Предмет:
Тема:
Теоремы сложения и умножения вероятностей
Вопрос:
Вероятность утери ценной книги библиотечным фондом в течение первого года после ее выпуска составляет 0,2, а в течение второго календарного года 0,3. Тогда вероятность того, что книга будет сохранена фондом в течение двух лет, равна …
Ответы:
+ 0,56
− 0,5
− 0,06
− 0,1
Решение:
Событие 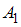 состоит в том, что книга будет утеряна в течение первого года после выпуска. Событие
состоит в том, что книга будет утеряна в течение первого года после выпуска. Событие 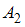 состоит в том, что книга будет утеряна в течение второго года. Согласно условию,
состоит в том, что книга будет утеряна в течение второго года. Согласно условию, 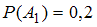 ,
, 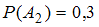 . Необходимо найти вероятность события
. Необходимо найти вероятность события 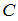 – сохранности книги в течение двух лет, то есть вероятность того, что имели место одновременно события
– сохранности книги в течение двух лет, то есть вероятность того, что имели место одновременно события 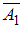 и
и 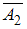 , противоположные событиям, рассмотренным выше.
, противоположные событиям, рассмотренным выше.
Вероятность события, противоположного данному, вычисляется по формуле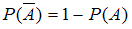 . Имеем:
. Имеем: 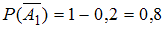 ,
, 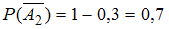 .
.
Событие, состоящее в одновременном появлении событий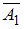 и
и 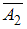 , называется их произведением. Используя формулу вероятности произведения событий, получим:
, называется их произведением. Используя формулу вероятности произведения событий, получим: 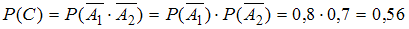 .
.
ответ тест i-exam
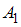 состоит в том, что книга будет утеряна в течение первого года после выпуска. Событие
состоит в том, что книга будет утеряна в течение первого года после выпуска. Событие 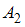 состоит в том, что книга будет утеряна в течение второго года. Согласно условию,
состоит в том, что книга будет утеряна в течение второго года. Согласно условию, 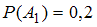 ,
, 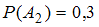 . Необходимо найти вероятность события
. Необходимо найти вероятность события 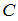 – сохранности книги в течение двух лет, то есть вероятность того, что имели место одновременно события
– сохранности книги в течение двух лет, то есть вероятность того, что имели место одновременно события 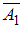 и
и 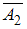 , противоположные событиям, рассмотренным выше.
, противоположные событиям, рассмотренным выше. Вероятность события, противоположного данному, вычисляется по формуле
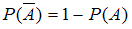 . Имеем:
. Имеем: 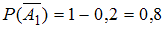 ,
, 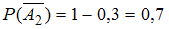 .
.Событие, состоящее в одновременном появлении событий
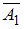 и
и 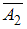 , называется их произведением. Используя формулу вероятности произведения событий, получим:
, называется их произведением. Используя формулу вероятности произведения событий, получим: 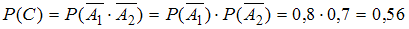 .
.ответ тест i-exam