Предмет:
Тема:
Теоремы сложения и умножения вероятностей
Вопрос:
В первой урне 5 синих шаров и 2 желтых, а во второй – 7 синих и 3 оранжевых. Из каждой урны случайным образом извлекается 1 шар. Вероятность того, что вынуты оба шара одного цвета, вычисляется следующим образом …
Ответы:
+ 
− 
− 
− 
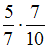
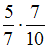
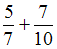
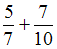
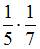
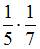
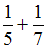
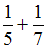
Решение:
Оба шара, вынутые из разных урн, могут иметь один и тот же цвет, если они синие.
Событие, состоящее в совместном появлении двух событий
и 
, называется произведением событий 
и 
.
Событие
состоит в том, что из первой урны извлечен синий шар. Вероятность этого события, согласно условию, 
.
Событие
состоит в том, что из второй урны извлечен синий шар.
Вероятность этого события, согласно условию,
.
Событие
– «из двух различных урн извлечены по одному шару одинакового цвета» – является произведением событий 
и 
.
События
и 
являются независимыми, поскольку урны различны, и результат извлечения шара из первой урны не оказывает влияния на результат извлечения шара из второй урны. Тогда, согласно теореме о нахождении вероятности произведения двух событий, имеем: 
.
ответ тест i-exam
Событие, состоящее в совместном появлении двух событий
и , называется произведением событий и .Событие
состоит в том, что из первой урны извлечен синий шар. Вероятность этого события, согласно условию, .Событие
состоит в том, что из второй урны извлечен синий шар. Вероятность этого события, согласно условию,
.Событие
– «из двух различных урн извлечены по одному шару одинакового цвета» – является произведением событий и .События
и являются независимыми, поскольку урны различны, и результат извлечения шара из первой урны не оказывает влияния на результат извлечения шара из второй урны. Тогда, согласно теореме о нахождении вероятности произведения двух событий, имеем: .ответ тест i-exam