Предмет:
Тема:
Законы распределения вероятностей непрерывных случайных величин. Нормальный закон распределения вероятностей
Вопрос:
Функция распределения для равномерно распределенной случайной величины задается формулой  . Ее график имеет вид:
. Ее график имеет вид:
Ответы:
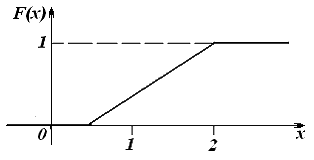
+ 

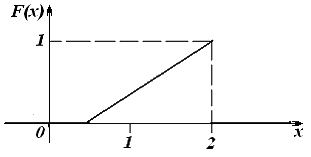
− 

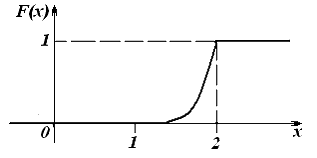
− 

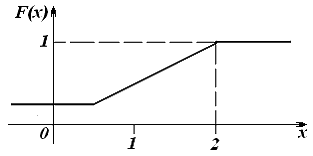
− 

Решение:
Согласно условию, функция распределения непрерывной случайной величины имеет вид:
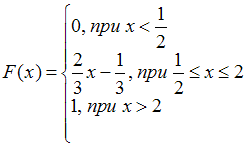 .
.
Таким образом, при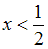 значение функции равно 0, то есть графически мы получим интервал вида
значение функции равно 0, то есть графически мы получим интервал вида 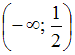 , принадлежащий оси абсцисс.
, принадлежащий оси абсцисс.
Так как при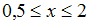 значение функции рассчитывается по формуле
значение функции рассчитывается по формуле 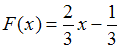 , то графически мы имеем отрезок прямой, концы которого находятся в точках
, то графически мы имеем отрезок прямой, концы которого находятся в точках 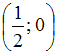 и
и 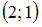 соответственно.
соответственно.
При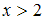 значение функции равно 1, то есть мы имеем луч, проходящий параллельно оси абсцисс в положительном направлении, с началом в точке
значение функции равно 1, то есть мы имеем луч, проходящий параллельно оси абсцисс в положительном направлении, с началом в точке 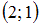 .
.
Этим условиям удовлетворяет только следующий график:
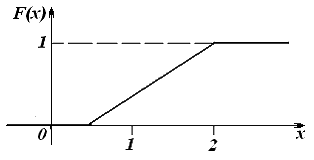 .
.
ответ тест i-exam
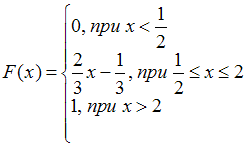 .
. Таким образом, при
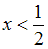 значение функции равно 0, то есть графически мы получим интервал вида
значение функции равно 0, то есть графически мы получим интервал вида 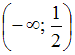 , принадлежащий оси абсцисс.
, принадлежащий оси абсцисс.Так как при
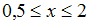 значение функции рассчитывается по формуле
значение функции рассчитывается по формуле 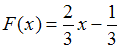 , то графически мы имеем отрезок прямой, концы которого находятся в точках
, то графически мы имеем отрезок прямой, концы которого находятся в точках 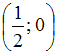 и
и 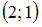 соответственно.
соответственно.При
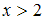 значение функции равно 1, то есть мы имеем луч, проходящий параллельно оси абсцисс в положительном направлении, с началом в точке
значение функции равно 1, то есть мы имеем луч, проходящий параллельно оси абсцисс в положительном направлении, с началом в точке 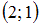 .
.Этим условиям удовлетворяет только следующий график:
 .
.ответ тест i-exam