Предмет:
Тема:
Законы распределения вероятностей непрерывных случайных величин. Нормальный закон распределения вероятностей
Вопрос:
Плотность распределения непрерывной случайной величины имеет вид: 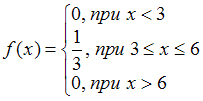 . Наименьшее значение, которое может принимать случайная величина
. Наименьшее значение, которое может принимать случайная величина 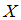 , равно …
, равно …
Ответы:
+ 3
− 5
− 6
− 7
Решение:
Требуется определить наименьшее значение, которое может принимать случайная величина 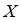 . Напомним, что функция плотности распределения, согласно условию, имеет вид:
. Напомним, что функция плотности распределения, согласно условию, имеет вид: 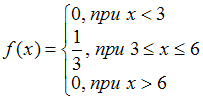 , и для нее справедливо условие:
, и для нее справедливо условие: 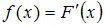 , где
, где 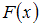 – функция распределения случайной величины. При
– функция распределения случайной величины. При 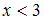 и
и 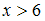 имеем
имеем 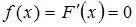 , то есть
, то есть 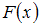 – некоторое число. Но, согласно свойствам функции распределения,
– некоторое число. Но, согласно свойствам функции распределения, 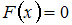 при
при 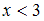 и
и 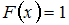 при
при 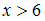 . Очевидно, что
. Очевидно, что 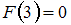 . Согласно определению, функция распределения
. Согласно определению, функция распределения 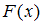 выражает вероятность того, что
выражает вероятность того, что 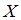 принимает значение, меньшее, чем
принимает значение, меньшее, чем 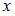 :
: 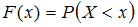 .
.
Вероятность принятия случайной величиной значения, которое меньше наименьшего из возможных значений, равна 0. Таким образом, наименьшее значение, принимаемое случайной величиной, равно 3.
ответ тест i-exam
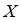 . Напомним, что функция плотности распределения, согласно условию, имеет вид:
. Напомним, что функция плотности распределения, согласно условию, имеет вид: 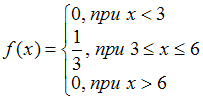 , и для нее справедливо условие:
, и для нее справедливо условие: 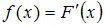 , где
, где 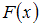 – функция распределения случайной величины. При
– функция распределения случайной величины. При 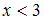 и
и 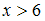 имеем
имеем 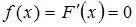 , то есть
, то есть 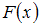 – некоторое число. Но, согласно свойствам функции распределения,
– некоторое число. Но, согласно свойствам функции распределения, 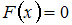 при
при 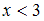 и
и 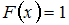 при
при 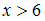 . Очевидно, что
. Очевидно, что 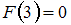 . Согласно определению, функция распределения
. Согласно определению, функция распределения 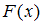 выражает вероятность того, что
выражает вероятность того, что 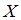 принимает значение, меньшее, чем
принимает значение, меньшее, чем 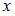 :
: 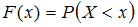 .
.Вероятность принятия случайной величиной значения, которое меньше наименьшего из возможных значений, равна 0. Таким образом, наименьшее значение, принимаемое случайной величиной, равно 3.
ответ тест i-exam