Предмет:
Тема:
Классическое определение вероятности
Вопрос:
В списке экзаменационных заданий 10 качественных задач и 16 количественных. Наудачу выбирается 2 задания. Вероятность того, что среди них будет только одна качественная задача, равна …
Ответы:
+ 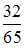
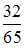
− 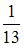
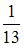
− 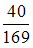
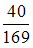
− 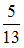
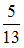
Решение:
Вероятностью события 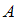 называется отношение числа элементарных исходов
называется отношение числа элементарных исходов 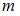 , благоприятствующих данному событию, к числу
, благоприятствующих данному событию, к числу 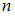 равновозможных элементарных исходов испытания:
равновозможных элементарных исходов испытания: 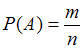 .
.
Из определения следует, что необходимо подсчитать число событий, благоприятных данному событию, и число равновозможных элементарных исходов.
В данной задаче событие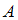 состоит в том, что из всех имеющихся заданий
состоит в том, что из всех имеющихся заданий 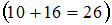 выбраны 2 задачи, среди которых 1 качественная задача и 1 количественная. Вычислим число благоприятных исходов. При выборе первой качественной задачи возможно 16 вариантов выбора количественной. Поскольку в списке 10 качественных задач, то общее число исходов, благоприятствующих событию
выбраны 2 задачи, среди которых 1 качественная задача и 1 количественная. Вычислим число благоприятных исходов. При выборе первой качественной задачи возможно 16 вариантов выбора количественной. Поскольку в списке 10 качественных задач, то общее число исходов, благоприятствующих событию 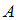 , равно
, равно 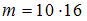 .
.
Общее число элементарных исходов определим, используя формулу для нахождения числа сочетаний из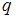 элементов по
элементов по 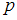 :
: 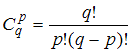 . Выясним, сколько существует способов выбора 2 заданий (
. Выясним, сколько существует способов выбора 2 заданий (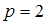 ) из 26 имеющихся (
) из 26 имеющихся (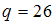 ).
).
Имеем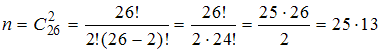 .
.
Итак,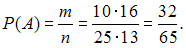
ответ тест i-exam
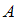 называется отношение числа элементарных исходов
называется отношение числа элементарных исходов 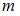 , благоприятствующих данному событию, к числу
, благоприятствующих данному событию, к числу 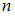 равновозможных элементарных исходов испытания:
равновозможных элементарных исходов испытания: 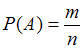 .
.Из определения следует, что необходимо подсчитать число событий, благоприятных данному событию, и число равновозможных элементарных исходов.
В данной задаче событие
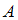 состоит в том, что из всех имеющихся заданий
состоит в том, что из всех имеющихся заданий 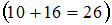 выбраны 2 задачи, среди которых 1 качественная задача и 1 количественная. Вычислим число благоприятных исходов. При выборе первой качественной задачи возможно 16 вариантов выбора количественной. Поскольку в списке 10 качественных задач, то общее число исходов, благоприятствующих событию
выбраны 2 задачи, среди которых 1 качественная задача и 1 количественная. Вычислим число благоприятных исходов. При выборе первой качественной задачи возможно 16 вариантов выбора количественной. Поскольку в списке 10 качественных задач, то общее число исходов, благоприятствующих событию 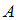 , равно
, равно 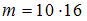 .
.Общее число элементарных исходов определим, используя формулу для нахождения числа сочетаний из
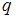 элементов по
элементов по 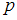 :
: 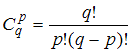 . Выясним, сколько существует способов выбора 2 заданий (
. Выясним, сколько существует способов выбора 2 заданий (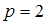 ) из 26 имеющихся (
) из 26 имеющихся (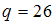 ).
).Имеем
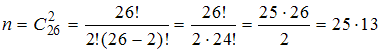 .
.Итак,
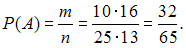
ответ тест i-exam