Предмет:
Тема:
Законы распределения вероятностей непрерывных случайных величин. Нормальный закон распределения вероятностей
Вопрос:
Интегральная функция распределения непрерывной случайной величины имеет вид: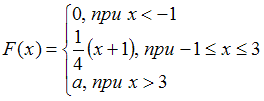 
. Тогда значение 
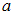равно …
Ответы:
+ 1
− 0
− 
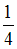
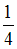
− 3
Решение:
Согласно определению, непрерывная случайная величина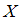 
задается функцией распределения 
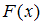, выражающей вероятность того, что 
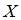принимает значение, меньшее, чем 
:
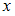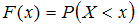. Причем первое значение, указанное в ограничениях относительно 
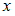, является наименьшим, а последнее – наибольшим из тех, которые может принимать случайная величина.
Согласно условию,
,
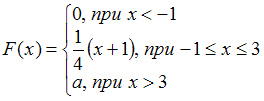то есть, наибольшее значение, которое может принимать случайная величина, равно 3. Таким образом, искомое значение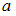
указывает вероятность того, что случайная величина принимает значение, не большее 3. Но она в любом случае не может принять значение, превышающее 3, поэтому данное событие достоверно, то есть его вероятность равна 1: 
.
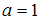ответ тест i-exam
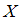задается функцией распределения 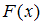, выражающей вероятность того, что 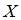принимает значение, меньшее, чем 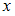: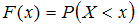. Причем первое значение, указанное в ограничениях относительно 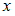, является наименьшим, а последнее – наибольшим из тех, которые может принимать случайная величина.Согласно условию,
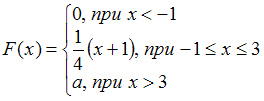,то есть, наибольшее значение, которое может принимать случайная величина, равно 3. Таким образом, искомое значение
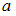указывает вероятность того, что случайная величина принимает значение, не большее 3. Но она в любом случае не может принять значение, превышающее 3, поэтому данное событие достоверно, то есть его вероятность равна 1: 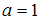.ответ тест i-exam