Предмет:
Тема:
Законы распределения вероятностей непрерывных случайных величин. Нормальный закон распределения вероятностей
Вопрос:
Наибольшее значение, принимаемое непрерывной случайной величиной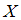 
, равно 3. Функция ее плотности распределения может иметь вид …
Ответы:
+ 
− 
− 
− 
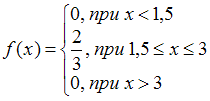
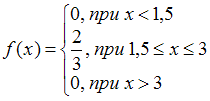
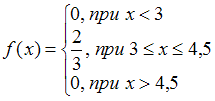
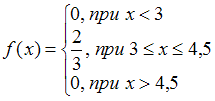
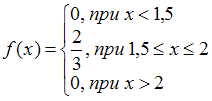
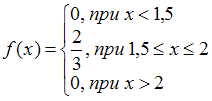
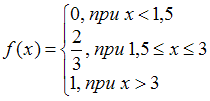
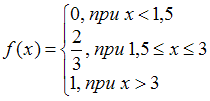
Решение:
Для плотности распределения непрерывной случайной величины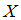 
справедливо условие: 
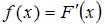, где 
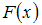– функция распределения случайной величины. Согласно определению, непрерывная случайная величина 
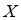задается функцией распределения 
, выражающей вероятность того, что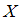 
принимает значение, меньшее, чем 
: 
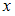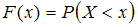. Если 
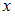– наибольшее значение, принимаемое случайной величиной, то 
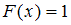, поэтому 
.
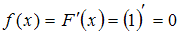Таким образом, нас устраивает только такой вид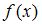
, который включает условие 
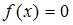при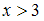 
. Этому условию удовлетворяет функция: 
.
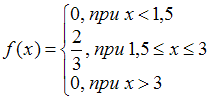Заметим, что функция вида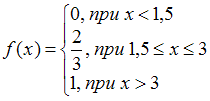
не является плотностью распределения, так как не выполняется условие 
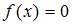при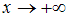 
.
Функция вида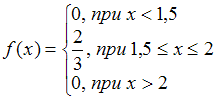
задает плотность распределения случайной величины 
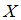, наибольшее значение которой равно 2, так как выполняется условие 
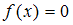при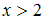 
. Таким образом, она не удовлетворяет требованию задачи.
Верный ответ: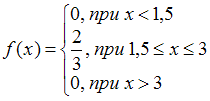
.
ответ тест i-exam
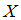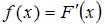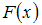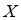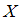справедливо условие: , где – функция распределения случайной величины. Согласно определению, непрерывная случайная величина задается функцией распределения , выражающей вероятность того, что принимает значение, меньшее, чем 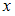: 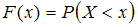. Если 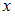– наибольшее значение, принимаемое случайной величиной, то 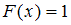, поэтому 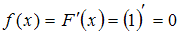.Таким образом, нас устраивает только такой вид
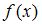, который включает условие 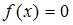при 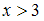. Этому условию удовлетворяет функция: 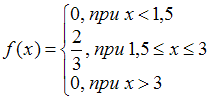.Заметим, что функция вида
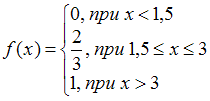не является плотностью распределения, так как не выполняется условие 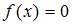при 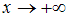.Функция вида
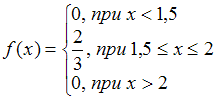задает плотность распределения случайной величины 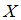, наибольшее значение которой равно 2, так как выполняется условие 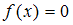при 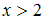. Таким образом, она не удовлетворяет требованию задачи.Верный ответ:
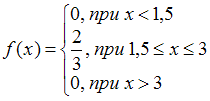.ответ тест i-exam