Предмет:
Тема:
Классическое определение вероятности
Вопрос:
Бросают 2 игральные кости. Вероятность того, что выпадет не менее 11 очков, равна …
Ответы:
+ 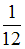
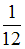
− 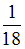
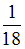
− 

− 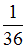
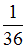
Решение:
Вероятностью события 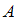 называется отношение числа элементарных исходов
называется отношение числа элементарных исходов 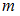 , благоприятствующих данному событию, к числу
, благоприятствующих данному событию, к числу 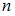 равновозможных элементарных исходов испытания:
равновозможных элементарных исходов испытания: 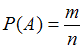 .
.
Из определения следует, что необходимо подсчитать число событий, благоприятных данному событию, и число равновозможных элементарных исходов.
Вычислим число благоприятных исходов. При броске 2 игральных костей может выпасть не менее 11 очков, то есть выпадет 11 или 12 очков. Это возможно в следующих случаях: когда на 2 костях одновременно выпадет по 6 очков (всего 12 очков), когда на первой кости выпадет 5 очков, а на второй – 6 (всего 11 очков) или когда на первой кости выпадет 6 очков, а на второй – 5 (всего 11 очков). Следовательно,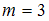 .
.
Общее число элементарных исходов определим, исходя из следующих рассуждений. Пусть на первой кости выпало 1 очко. На второй может выпасть 1, 2, 3, 4, 5 или 6 очков. Таким образом, для каждой выпавшей грани одной игральной кости может выпасть одна из 6 граней на другой. Поэтому общее число исходов определяется формулой: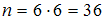 . Итак,
. Итак, 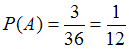 .
.
ответ тест i-exam
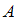 называется отношение числа элементарных исходов
называется отношение числа элементарных исходов 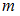 , благоприятствующих данному событию, к числу
, благоприятствующих данному событию, к числу 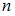 равновозможных элементарных исходов испытания:
равновозможных элементарных исходов испытания: 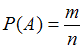 .
.Из определения следует, что необходимо подсчитать число событий, благоприятных данному событию, и число равновозможных элементарных исходов.
Вычислим число благоприятных исходов. При броске 2 игральных костей может выпасть не менее 11 очков, то есть выпадет 11 или 12 очков. Это возможно в следующих случаях: когда на 2 костях одновременно выпадет по 6 очков (всего 12 очков), когда на первой кости выпадет 5 очков, а на второй – 6 (всего 11 очков) или когда на первой кости выпадет 6 очков, а на второй – 5 (всего 11 очков). Следовательно,
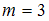 .
.Общее число элементарных исходов определим, исходя из следующих рассуждений. Пусть на первой кости выпало 1 очко. На второй может выпасть 1, 2, 3, 4, 5 или 6 очков. Таким образом, для каждой выпавшей грани одной игральной кости может выпасть одна из 6 граней на другой. Поэтому общее число исходов определяется формулой:
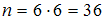 . Итак,
. Итак, 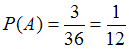 .
.ответ тест i-exam