Предмет:
Тема:
Теоремы сложения и умножения вероятностей
Вопрос:
На стеллаже были выставлены 10-томное собрание сочинений Пушкина, три тома Дюма и 5 томов Лермонтова. Посетитель библиотеки наугад выбирает один из томов. Вероятность выбора произведения классика русской литературы равна …
Ответы:
+ 
− 
− 
− 
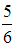
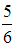
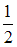
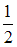
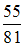
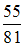
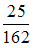
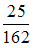
Решение:
Событие, состоящее в появлении хотя бы одного из событий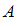 
и 
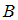, называется суммой событи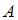й 
и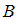 
. Вероятность суммы двух несовместных событи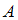й 
и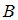 
вычисляется согласно формуле: 
.
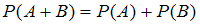Рассмотрим событие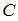
– наугад выбрано произведение классика русской литературы. Это может произойти в случае выбора тома Пушкина или книги Лермонтова. Пусть событие 
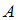состоит в том, что выбрано произведение Пушкина, а событие 
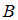состоит в том, что выбрано произведение Лермонтова. На полке 
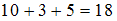книг. Таким образом, событие 
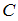является суммой событи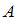й 
и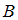 
. Согласно условию, произведения Пушкина составляют 10 книг из 18, а Лермонтова – 5 книг из 18. Поэтому 
, 
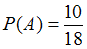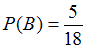. События 
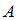и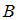 
являются несовместными, поскольку среди книг не было сборников произведений различных авторов. Тогда искомая вероятность равна: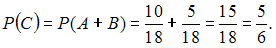 
ответ тест i-exam
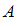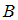и , называется суммой событи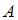й и 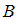. Вероятность суммы двух несовместных событи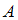й и 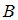вычисляется согласно формуле: 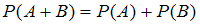.Рассмотрим событие
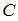– наугад выбрано произведение классика русской литературы. Это может произойти в случае выбора тома Пушкина или книги Лермонтова. Пусть событие 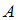состоит в том, что выбрано произведение Пушкина, а событие 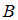состоит в том, что выбрано произведение Лермонтова. На полке 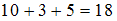книг. Таким образом, событие 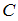является суммой событи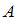й и 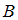. Согласно условию, произведения Пушкина составляют 10 книг из 18, а Лермонтова – 5 книг из 18. Поэтому 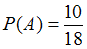, 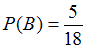. События 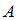и 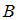являются несовместными, поскольку среди книг не было сборников произведений различных авторов. Тогда искомая вероятность равна: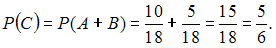 ответ тест i-exam