Предмет:
Тема:
Основные понятия теории множеств
Вопрос:
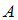– множество чисел, оканчивающихся на 6, 
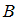– множество четных чисел. Тогда о множествах 
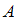и 
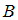можно сказать, что …
Ответы:
+ 
+ 
− 
− 
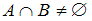
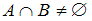
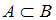
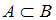
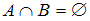
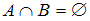
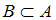
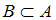
Решение:
Множество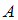 
включено во множество 
(
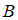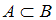), если каждый элемент множества 
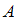одновременно является элементом множества 
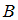. Множества 
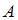и 
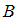не пересекаются (
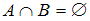), если они не имеют общих элементов. Множества 
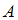и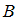 
пересекаются (
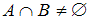), если у них есть общие элементы.
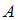– множество чисел, оканчивающихся на 6, 
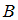– множество четных чисел. Множества 
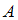и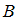 
пересекаются, так как у них есть общие элементы – это четные числа, оканчивающиеся на 6, например, 16, 536, 4796. Значит, высказывание 
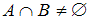истинно, а высказывание 
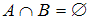ложно.
Любое число, оканчивающееся на 6, является четным, то есть каждый элемент множества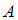
одновременно является элементом множества 
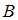, значит, 
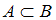, то есть высказывание 
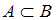истинно. Но нельзя сказать, что любое четное число оканчивается на 6, то есть высказывание 
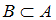ложно.
Таким образом, истинны высказывания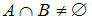
и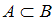 
.
ответ тест i-exam
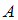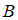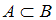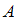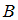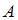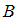включено во множество (), если каждый элемент множества одновременно является элементом множества . Множества и не пересекаются (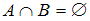), если они не имеют общих элементов. Множества 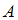и 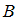пересекаются (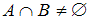), если у них есть общие элементы. 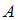– множество чисел, оканчивающихся на 6, 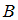– множество четных чисел. Множества 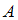и 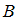пересекаются, так как у них есть общие элементы – это четные числа, оканчивающиеся на 6, например, 16, 536, 4796. Значит, высказывание 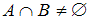истинно, а высказывание 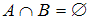ложно.Любое число, оканчивающееся на 6, является четным, то есть каждый элемент множества
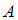одновременно является элементом множества 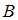, значит, 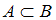, то есть высказывание 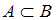истинно. Но нельзя сказать, что любое четное число оканчивается на 6, то есть высказывание 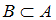ложно.Таким образом, истинны высказывания
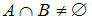и 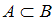.ответ тест i-exam