Предмет:
Тема:
Формула полной вероятности и формула Бейеса
Вопрос:
Два преподавателя проверяют работы письменного экзамена по математике. Вероятность того, что работа попадет к первому преподавателю (событие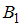 
), равна 0,55, ко второму (событие 
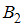) – 0,45. Вероятность того, что первый преподаватель забудет заверить проверенную работу, равна 0,04, а второй – 0,02. Для расчета вероятности того, что выбранная наудачу работа не была заверена (событие 
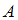), используется формула полной вероятности 
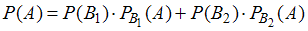. Установите соответствие между обозначениями вероятностей и их числовыми значениями:
1) 
,
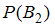2) 
,
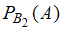3) 
.
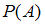Ответы:
1 0,45
2 0,02
3 0,031
0,022
Решение:
Событие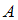 
– выбранная наудачу работа не была заверена – рассматривается при условии, что она была проверена первым преподавателем (событие 
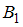) либо вторым (событие 
).
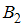Для решения задачи используется формула полной вероятности: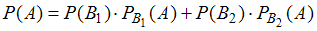
. Событие 
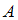совершается с одним из двух несовместных событий 
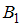или 
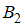. Таким образом, 
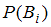– вероятность события 
; 
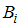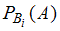– условная вероятность события 
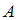, то есть вероятность события 
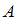, вычисленная в предположении, что событие 
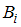наступило.
Согласно условию, вероятность того, что работа проверена первым преподавателем,
, а вероятность того, что в этом случае работа не будет заверена,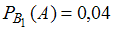 
.
Вероятность того, что работа проверена вторым преподавателем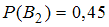
, а вероятность того, что в этом случае работа не будет заверена 
.
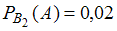Подставив данные в формулу полной вероятности, имеем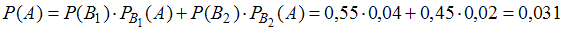
.
Следовательно, имеем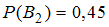
, 
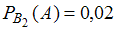и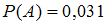 
.
ответ тест i-exam
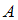– выбранная наудачу работа не была заверена – рассматривается при условии, что она была проверена первым преподавателем (событие 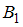) либо вторым (событие 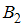).Для решения задачи используется формула полной вероятности:
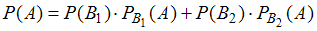. Событие 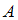совершается с одним из двух несовместных событи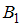й или 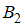. Таким образом, 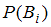– вероятность события 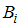; 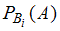– условная вероятность события 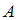, то есть вероятность события 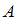, вычисленная в предположении, что событие 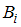наступило.Согласно условию, вероятность того, что работа проверена первым преподавателем,
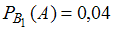, а вероятность того, что в этом случае работа не будет заверена, .Вероятность того, что работа проверена вторым преподавателем
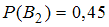, а вероятность того, что в этом случае работа не будет заверена 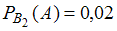.Подставив данные в формулу полной вероятности, имеем
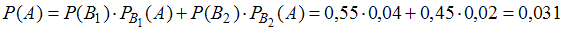.Следовательно, имеем
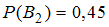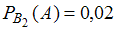, и 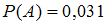.ответ тест i-exam
Похожие вопросы:
