Предмет:
Тема:
Характеристики вариационного ряда: мода и медиана
Вопрос:
Размах выборки, имеющей статистическое распределение
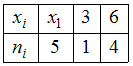
равен 5. Тогда медиана выборки равна …
Ответы:
+ 2
− 1
− 3
− 4
Решение:
Статистическим распределением выборки называют перечень вариант 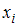 и соответствующих им частот
и соответствующих им частот 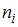 , который записывается в виде таблицы:
, который записывается в виде таблицы: 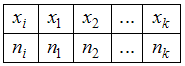
Размах вариации – разность наибольшего и наименьшего значений вариант. Согласно условию,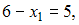 отсюда
отсюда 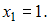
Статистическое распределение выборки принимает вид:
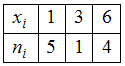
Медиана – это значение признака, приходящееся на середину вариационного ряда. Наблюдаемые значения рассматриваемого признака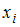 называются вариантами. Количество наблюдений данной варианты – частота
называются вариантами. Количество наблюдений данной варианты – частота 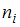 . Число объектов выборочной совокупности называется объемом выборки
. Число объектов выборочной совокупности называется объемом выборки 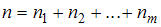 , где
, где 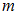 – количество вариант. Если объем выборки
– количество вариант. Если объем выборки 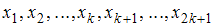 – нечетное число, то есть
– нечетное число, то есть 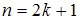 , то медианой является варианта
, то медианой является варианта 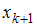 ; если объем выборки
; если объем выборки 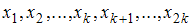 – четное число, то есть
– четное число, то есть 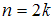 , медиана равна
, медиана равна 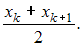
Объем выборки, представленной данным статистическим распределением, равен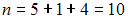 – четное число, поэтому
– четное число, поэтому 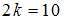 . Отсюда
. Отсюда 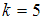 , то есть медиана равна
, то есть медиана равна 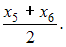
В нашем случае: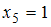 ,
, 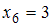 . Тогда значение медианы
. Тогда значение медианы 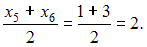
ответ тест i-exam
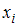 и соответствующих им частот
и соответствующих им частот 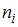 , который записывается в виде таблицы:
, который записывается в виде таблицы: 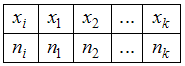
Размах вариации – разность наибольшего и наименьшего значений вариант. Согласно условию,
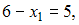 отсюда
отсюда 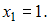
Статистическое распределение выборки принимает вид:
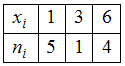
Медиана – это значение признака, приходящееся на середину вариационного ряда. Наблюдаемые значения рассматриваемого признака
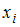 называются вариантами. Количество наблюдений данной варианты – частота
называются вариантами. Количество наблюдений данной варианты – частота 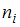 . Число объектов выборочной совокупности называется объемом выборки
. Число объектов выборочной совокупности называется объемом выборки 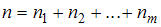 , где
, где 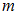 – количество вариант. Если объем выборки
– количество вариант. Если объем выборки 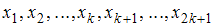 – нечетное число, то есть
– нечетное число, то есть 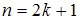 , то медианой является варианта
, то медианой является варианта 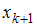 ; если объем выборки
; если объем выборки 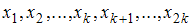 – четное число, то есть
– четное число, то есть 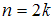 , медиана равна
, медиана равна 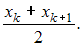
Объем выборки, представленной данным статистическим распределением, равен
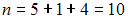 – четное число, поэтому
– четное число, поэтому 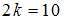 . Отсюда
. Отсюда 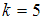 , то есть медиана равна
, то есть медиана равна 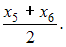
В нашем случае:
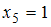 ,
, 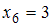 . Тогда значение медианы
. Тогда значение медианы 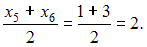
ответ тест i-exam