Предмет:
Тема:
Определенный интеграл. Формула Ньютона - Лейбница
Вопрос:
Определенный интеграл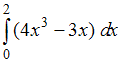 
равен …
Ответы:
+ 10
− 45
− 26
− 16
Решение:
Определенный интеграл от непрерывной на отрезке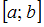 
функции можно вычислить с помощью формулы Ньютона – Лейбница:
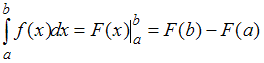, где 
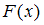– любая первообразная функции 
.
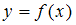Для вычисления данного определенного интеграла необходимо использовать табличный интеграл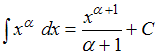
, где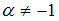 
и линейные свойства интеграла: 1) постоянный множитель можно выносить за знак интеграла 
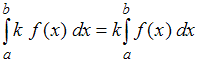; 2) интеграл алгебраической суммы (разности) двух функций равен сумме (разности) интегралов этих функций 
.
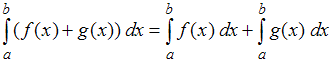Найдем неопределенный интеграл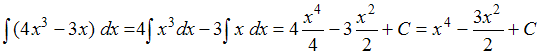
. Возьмем одну из полученных первообразных, например 
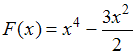, которая получается при 
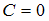. Так как подынтегральная функция 
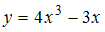непрерывна на отрезке 
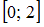и имеет на нем первообразную, то для вычисления определенного интеграла применим формулу Ньютона – Лейбница:
.
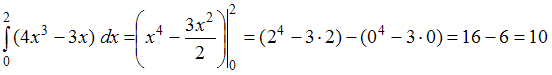ответ тест i-exam
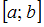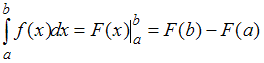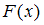функции можно вычислить с помощью формулы Ньютона – Лейбница:, где – любая первообразная функции 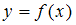.Для вычисления данного определенного интеграла необходимо использовать табличный интеграл
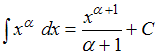, где 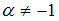и линейные свойства интеграла: 1) постоянный множитель можно выносить за знак интеграла 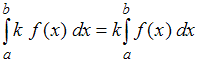; 2) интеграл алгебраической суммы (разности) двух функций равен сумме (разности) интегралов этих функций 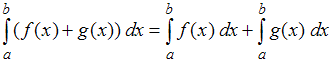.Найдем неопределенный интеграл
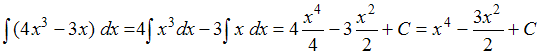. Возьмем одну из полученных первообразных, например 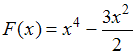, которая получается при 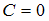. Так как подынтегральная функция 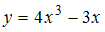непрерывна на отрезке 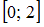и имеет на нем первообразную, то для вычисления определенного интеграла применим формулу Ньютона – Лейбница: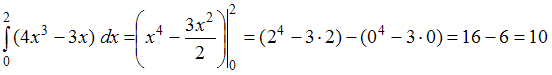.ответ тест i-exam
Похожие вопросы:
) равен 174 см, средний вес (
) равен 424 кг;. коэффициент регрессии (
) равен 6,4 кг/см, среднеквадратическое отклонение (s) по весу равно 56,8 кг, а по обхвату груди – 7,9 см; коэффициент наследуемости (h2) по весу равен 0,45.
) равен 174 см, средний вес (
) равен 424 кг, коэффициент регрессии (
) равен 6,4 кг/см, среднеквадратическое отклонение (s) по весу равно 56,8 кг, а по обхвату груди – 7,9 см; коэффициент наследуемости (h2) по весу равен 0,45. 
) равен 174 см, средний вес (
) равен 424 кг, коэффициент регрессии (
) равен 6,4 кг/см, среднеквадратическое отклонение (s) по весу равно 56,8 кг, а по обхвату груди – 7,9 см; коэффициент наследуемости (h2) по весу равен 0,45. 
) равен 174 см, средний вес (
) равен 424 кг;. коэффициент регрессии (
) равен 6,4 кг/см, среднеквадратическое отклонение (s) по весу равно 56,8 кг, а по обхвату груди – 7,9 см; коэффициент наследуемости (h2) по весу равен 0,45.
так, что оси кольца и стержня совпадают (рис.).
и радиальной 
составляющих вектора магнитной индукции от вертикальной 
и радиальной 
координаты имеют вид: 
, 
, где 
, 
и 
– постоянные. Кольцо отпускают, и оно начинает двигаться вниз. Первоначально ток в кольце был равен нулю. При этом справедливы следующие утверждения: ______.