Предмет:
Тема:
Дифференциальные уравнения с разделяющимися переменными
Вопрос:
Уравнение 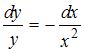 с разделенными переменными можно получить из уравнения …
с разделенными переменными можно получить из уравнения …
Ответы:
+ 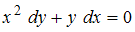
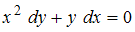
− 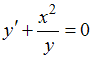
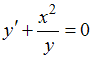
− 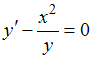
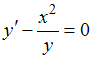
− 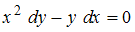
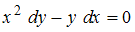
Решение:
Если дифференциальное уравнение имеет вид 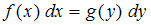 , то говорят, что переменные в нем разделены.
, то говорят, что переменные в нем разделены.
Проведем разделение переменных в каждом из уравнений, представив производную функции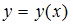 в виде
в виде 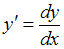 , и сравним полученные уравнения с уравнением
, и сравним полученные уравнения с уравнением 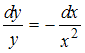 .
.
Преобразуем уравнение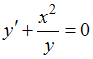 к виду
к виду 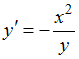 или
или 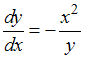 . Умножим обе части уравнения на
. Умножим обе части уравнения на 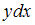 , получим уравнение с разделенными переменными
, получим уравнение с разделенными переменными 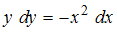 , которое не совпадает с предложенным уравнением.
, которое не совпадает с предложенным уравнением.
Преобразуем уравнение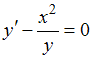 к виду
к виду 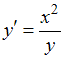 или
или 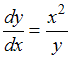 . Умножим обе части уравнения на
. Умножим обе части уравнения на 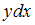 , получим уравнение с разделенными переменными
, получим уравнение с разделенными переменными 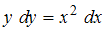 , которое также не совпадает с предложенным уравнением.
, которое также не совпадает с предложенным уравнением.
Преобразуем уравнение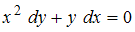 к виду
к виду 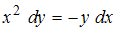 . Разделив обе части уравнения на
. Разделив обе части уравнения на 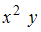 , получим уравнение с разделенными переменными
, получим уравнение с разделенными переменными 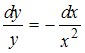 , которое совпадает с предложенным.
, которое совпадает с предложенным.
Преобразуем уравнение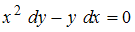 к виду
к виду 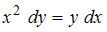 . Разделив обе части уравнения на
. Разделив обе части уравнения на 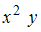 , получим уравнение с разделенными переменными
, получим уравнение с разделенными переменными 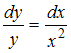 , которое не совпадает с предложенным.
, которое не совпадает с предложенным.
Следовательно, уравнение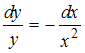 с разделенными переменными можно получить из уравнения
с разделенными переменными можно получить из уравнения 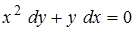 .
.
ответ тест i-exam
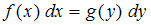 , то говорят, что переменные в нем разделены.
, то говорят, что переменные в нем разделены.Проведем разделение переменных в каждом из уравнений, представив производную функции
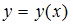 в виде
в виде 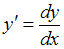 , и сравним полученные уравнения с уравнением
, и сравним полученные уравнения с уравнением 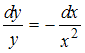 .
.Преобразуем уравнение
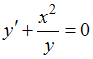 к виду
к виду 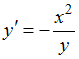 или
или 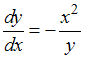 . Умножим обе части уравнения на
. Умножим обе части уравнения на 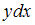 , получим уравнение с разделенными переменными
, получим уравнение с разделенными переменными 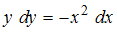 , которое не совпадает с предложенным уравнением.
, которое не совпадает с предложенным уравнением.Преобразуем уравнение
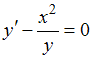 к виду
к виду 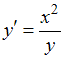 или
или 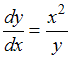 . Умножим обе части уравнения на
. Умножим обе части уравнения на 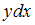 , получим уравнение с разделенными переменными
, получим уравнение с разделенными переменными 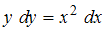 , которое также не совпадает с предложенным уравнением.
, которое также не совпадает с предложенным уравнением.Преобразуем уравнение
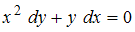 к виду
к виду 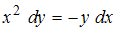 . Разделив обе части уравнения на
. Разделив обе части уравнения на 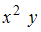 , получим уравнение с разделенными переменными
, получим уравнение с разделенными переменными 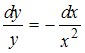 , которое совпадает с предложенным.
, которое совпадает с предложенным.Преобразуем уравнение
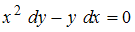 к виду
к виду 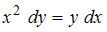 . Разделив обе части уравнения на
. Разделив обе части уравнения на 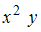 , получим уравнение с разделенными переменными
, получим уравнение с разделенными переменными 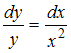 , которое не совпадает с предложенным.
, которое не совпадает с предложенным.Следовательно, уравнение
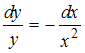 с разделенными переменными можно получить из уравнения
с разделенными переменными можно получить из уравнения 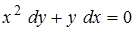 .
.ответ тест i-exam