Предмет:
Тема:
Дифференциальные уравнения с разделяющимися переменными
Вопрос:
Общий интеграл дифференциального уравнения с разделенными переменными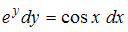 
имеет вид …
Ответы:
+ 
− 
− 
− 
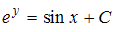
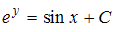
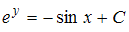
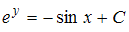
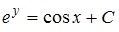
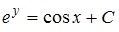
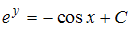
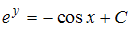
Решение:
Если дифференциальное уравнение имеет вид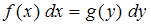 
, то говорят, что переменные в нем разделены. Такое уравнение решается путем интегрирования обеих частей уравнения: 
.
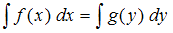Если G(y) – какая-нибудь первообразная функция для g(y), а F(x) – первообразная для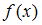
, то общее решение данного уравнения можно записать в виде: 
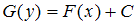, где 
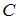– произвольная постоянная.
Проинтегрируем обе части уравнения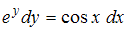
, получим 
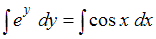. Так как 
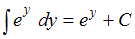и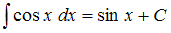 
, то общий интеграл дифференциального уравнения будет иметь вид 
.
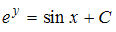ответ тест i-exam
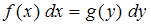, то говорят, что переменные в нем разделены. Такое уравнение решается путем интегрирования обеих частей уравнения: 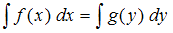.Если G(y) – какая-нибудь первообразная функция для g(y), а F(x) – первообразная для
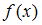, то общее решение данного уравнения можно записать в ви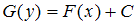де: , где 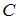– произвольная постоянная.Проинтегрируем обе части уравнения
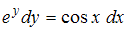, получим 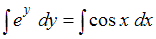. Так как 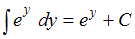и 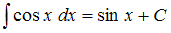, то общий интеграл дифференциального уравнения будет иметь вид 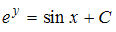.ответ тест i-exam