Предмет:
Тема:
Определенный интеграл. Формула Ньютона - Лейбница
Вопрос:
Определенный интеграл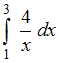 
равен …
Ответы:
+ 
− 
− 
− 
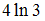
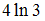
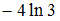
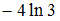
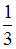
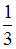
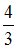
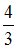
Решение:
Определенный интеграл от непрерывной на отрезке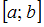 
функции можно вычислить с помощью формулы Ньютона – Лейбница:
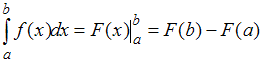, где 
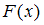– любая первообразная функции 
.
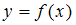Для вычисления данного определенного интеграла необходимо использовать свойство определенного интеграла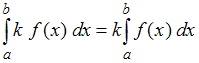
, где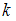 
– некоторое число, а также учесть, что функция 
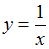на отрезке 
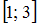имеет первообразную 
.
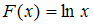Подынтегральная функция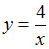
непрерывна на отрезке 
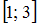, следовательно, для вычисления определенного интеграла можно применить формулу Ньютона – Лейбница:
.
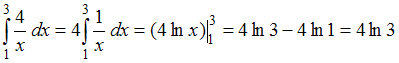(Напомним, что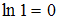
).
ответ тест i-exam
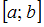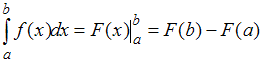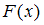функции можно вычислить с помощью формулы Ньютона – Лейбница:, где – любая первообразная функции 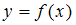.Для вычисления данного определенного интеграла необходимо использовать свойство определенного интеграла
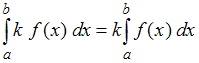, где 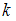– некоторое число, а также учесть, что функция 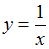на отрезке 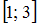имеет первообразную 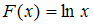.Подынтегральная функция
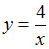непрерывна на отрезке 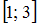, следовательно, для вычисления определенного интеграла можно применить формулу Ньютона – Лейбница: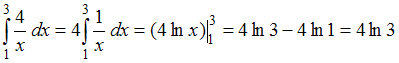.(Напомним, что
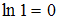).ответ тест i-exam