Предмет:
Тема:
Дифференциальное исчисление. Формулы, основные правила дифференцирования
Вопрос:
Среди предложенных равенств неверным является …
Ответы:
+ 
− 
− 
− 
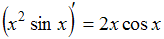
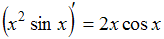
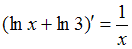
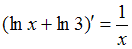
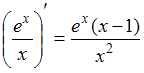
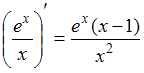
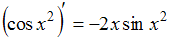
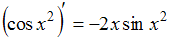
Решение:
Выясним правильность нахождения производных в каждом случае.
Рассмотрим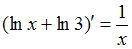
. Функция 
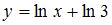представляет собой сумму двух функций, поэтому ее производную находят по формуле 
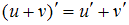. Производная первого слагаемого находится по формуле 
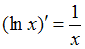. Так как 
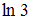– это постоянная, то 
. 
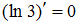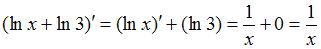. Таким образом, предложенное равенство является верным.
Проверим равенство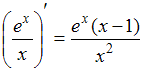
.
Функция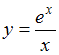
представляет собой частное двух функций, поэтому производную находим по формуле производной частного 
.
.
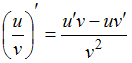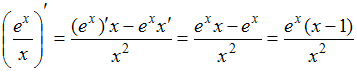Таким образом, предложенное равенство является верным.
Рассмотрим равенство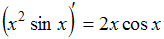
. Функция 
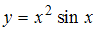представляет собой произведение двух функций, поэтому производную находим по формуле производной произведения 
.
.
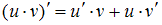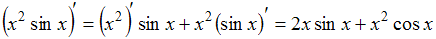Таким образом, предложенное равенство является неверным.
Проверим равенство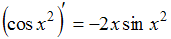
. Функция 
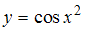является сложной, поэтому ее производную находим по формуле производной сложной функции 
.
.
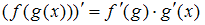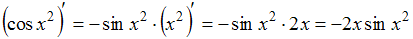Таким образом, предложенное равенство является верным.
Следовательно, неверным является равенство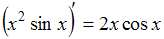
.
ответ тест i-exam
Рассмотрим
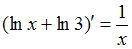. Функция 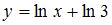представляет собой сумму двух функций, поэтому ее производную находят по формуле 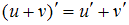. Производная первого слагаемого находится по формуле 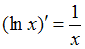. Так как 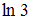– это постоянная, то 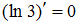. . 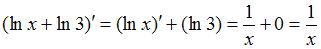Таким образом, предложенное равенство является верным.Проверим равенство
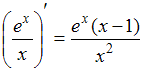.Функция
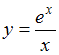представляет собой частное двух функций, поэтому производную находим по формуле производной частного 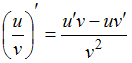..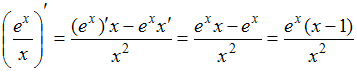Таким образом, предложенное равенство является верным.
Рассмотрим равенство
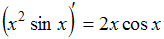. Функция 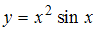представляет собой произведение двух функций, поэтому производную находим по формуле производной произведения 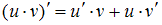..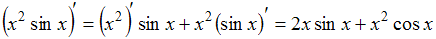Таким образом, предложенное равенство является неверным.
Проверим равенство
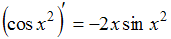. Функция 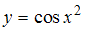является сложной, поэтому ее производную находим по формуле производной сложной функции 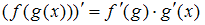..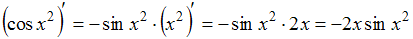Таким образом, предложенное равенство является верным.
Следовательно, неверным является равенство
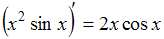.ответ тест i-exam