Предмет:
Тема:
Точечные оценки параметров распределения
Вопрос:
Выборочная дисперсия выборки, заданной вариационным рядом 1, 1, 1, 2, 3, 3, 4, 4, 4, 7, равна …
Ответы:
+ 3,2
− 3,4
− 0,6
− 3
Решение:
Для расчета выборочной дисперсии воспользуемся формулой: 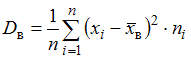 . Вспомним смысл статистических понятий, входящих в состав данной формулы.
. Вспомним смысл статистических понятий, входящих в состав данной формулы.
Согласно определению, выборочной средней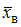 называют среднее арифметическое значение признака выборочной совокупности, которое вычисляют по формуле
называют среднее арифметическое значение признака выборочной совокупности, которое вычисляют по формуле 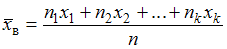 , где
, где 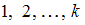 – номера вариант, а
– номера вариант, а 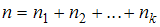 – объем выборки. Наблюдаемые значения рассматриваемого признака
– объем выборки. Наблюдаемые значения рассматриваемого признака 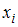 называются вариантами. Количество наблюдений данной варианты – частота
называются вариантами. Количество наблюдений данной варианты – частота 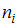 .
.
Согласно условию, варианты и их частоты имеют вид: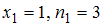 ,
, 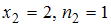 ,
, 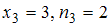 ,
, 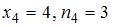 ,
, 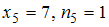 .
.
Объем выборки равен: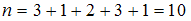 .
.
Выборочная средняя: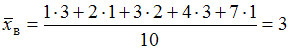 .
.
Выборочная дисперсия: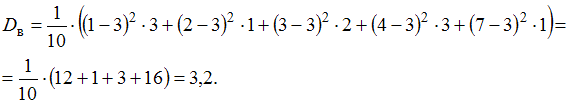
ответ тест i-exam
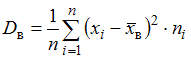 . Вспомним смысл статистических понятий, входящих в состав данной формулы.
. Вспомним смысл статистических понятий, входящих в состав данной формулы.Согласно определению, выборочной средней
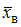 называют среднее арифметическое значение признака выборочной совокупности, которое вычисляют по формуле
называют среднее арифметическое значение признака выборочной совокупности, которое вычисляют по формуле 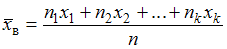 , где
, где 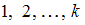 – номера вариант, а
– номера вариант, а 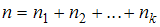 – объем выборки. Наблюдаемые значения рассматриваемого признака
– объем выборки. Наблюдаемые значения рассматриваемого признака 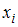 называются вариантами. Количество наблюдений данной варианты – частота
называются вариантами. Количество наблюдений данной варианты – частота 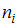 .
.Согласно условию, варианты и их частоты имеют вид:
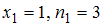 ,
, 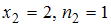 ,
, 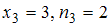 ,
, 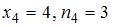 ,
, 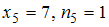 .
.Объем выборки равен:
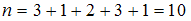 .
.Выборочная средняя:
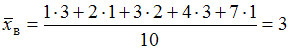 .
.Выборочная дисперсия:
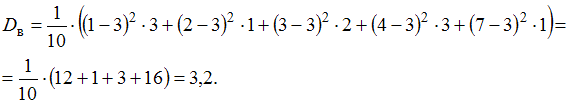
ответ тест i-exam