Предмет:
Тема:
Правило суммы и произведения
Вопрос:
Количество всевозможных трехзначных чисел, кратных 5, равно …
Ответы:
+180
Решение:
Если какой-либо объект можно выбрать 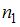 способами, второй объект –
способами, второй объект – 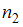 способами и так далее, а
способами и так далее, а 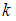 -й объект –
-й объект – 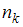 способами, то по правилу произведения
способами, то по правилу произведения 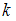 упорядоченных объектов можно выбрать
упорядоченных объектов можно выбрать 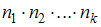 способами.
способами.
Число кратно 5 (делится на 5), если оно оканчивается цифрой 0 или 5. Значит, третья цифра нашего трехзначного числа должна быть равна 0 или 5, то есть ее можно выбрать 2 способами. Первую цифру числа можно выбрать 9 способами (любая цифра, кроме 0), вторую цифру можно выбрать 10 способами (любая из 10 цифр). Значит, количество искомых трехзначных чисел по правилу произведения будет равно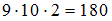 .
.
ответ тест i-exam
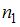 способами, второй объект –
способами, второй объект – 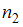 способами и так далее, а
способами и так далее, а 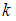 -й объект –
-й объект – 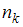 способами, то по правилу произведения
способами, то по правилу произведения 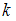 упорядоченных объектов можно выбрать
упорядоченных объектов можно выбрать 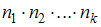 способами.
способами.Число кратно 5 (делится на 5), если оно оканчивается цифрой 0 или 5. Значит, третья цифра нашего трехзначного числа должна быть равна 0 или 5, то есть ее можно выбрать 2 способами. Первую цифру числа можно выбрать 9 способами (любая цифра, кроме 0), вторую цифру можно выбрать 10 способами (любая из 10 цифр). Значит, количество искомых трехзначных чисел по правилу произведения будет равно
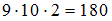 .
.ответ тест i-exam