Предмет:
Тема:
Правило суммы и произведения
Вопрос:
Из цифр 1, 2, 3, 4, 5, 6 составляются всевозможные четные трехзначные числа так, чтобы первая и последняя цифра в каждом из этих чисел были одинаковы (например, 454). Тогда количество таких чисел будет равно …
Ответы:
+18
Решение:
Так как в искомых трехзначных числах первая и последняя цифра должны быть одинаковы, то нам достаточно выбрать только вторую и третью цифры числа (первая цифра будет равна третьей).
По правилу произведения если какой-либо объект можно выбрать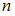 способами, а второй объект после выбора первого –
способами, а второй объект после выбора первого – 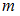 способами, то упорядоченную пару объектов можно выбрать
способами, то упорядоченную пару объектов можно выбрать 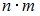 способами.
способами.
Так как искомые трехзначные числа должны быть четными, то последняя их цифра должна быть четной. Значит, третью цифру числа из цифр 1, 2, 3, 4, 5, 6 можно выбрать 3 способами (2, 4 или 6). Вторую цифру можно выбрать 6 способами (любая из 6 цифр). Таким образом, количество искомых трехзначных чисел по правилу произведения будет равно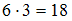 .
.
ответ тест i-exam
По правилу произведения если какой-либо объект можно выбрать
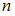 способами, а второй объект после выбора первого –
способами, а второй объект после выбора первого – 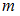 способами, то упорядоченную пару объектов можно выбрать
способами, то упорядоченную пару объектов можно выбрать 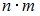 способами.
способами.Так как искомые трехзначные числа должны быть четными, то последняя их цифра должна быть четной. Значит, третью цифру числа из цифр 1, 2, 3, 4, 5, 6 можно выбрать 3 способами (2, 4 или 6). Вторую цифру можно выбрать 6 способами (любая из 6 цифр). Таким образом, количество искомых трехзначных чисел по правилу произведения будет равно
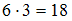 .
.ответ тест i-exam