Предмет:
Тема:
Формула полной вероятности и формула Бейеса
Вопрос:
Два программиста вводят данные по 20 представленным статистическим таблицам. Вероятность ошибки при вводе данных для первого программиста составляет 0,1, а для второго – 0,2. Первый программист работает с 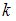 таблицами, а остальные таблицы обрабатываются вторым программистом.
таблицами, а остальные таблицы обрабатываются вторым программистом.
Установите соответствие между значением 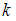 и вероятностью ошибки в случайно выбранной электронной таблице:
и вероятностью ошибки в случайно выбранной электронной таблице:
1) 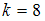 ,
,
2) 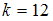 .
.
Ответы:
1 0,16
2 0,14
0,56
Решение:
Рассмотрим событие 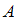 – случайно выбранная таблица содержит ошибку ввода. Оно может произойти при обработке данных как первым программистом (событие
– случайно выбранная таблица содержит ошибку ввода. Оно может произойти при обработке данных как первым программистом (событие 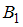 ), так и вторым (событие
), так и вторым (событие 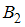 ). Заметим, что события
). Заметим, что события 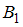 и
и 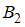 несовместны, поскольку с таблицей не могут работать два человека сразу, и противоположны, так как других вариантов для обработки материалов нет. Поэтому вероятность события
несовместны, поскольку с таблицей не могут работать два человека сразу, и противоположны, так как других вариантов для обработки материалов нет. Поэтому вероятность события 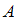 может быть определена при помощи формулы полной вероятности:
может быть определена при помощи формулы полной вероятности: 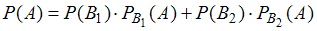 , где
, где 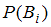 – вероятность события
– вероятность события 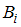 ;
; 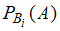 – условная вероятность события
– условная вероятность события 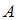 , то есть вероятность события
, то есть вероятность события 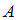 , вычисленная в предположении, что событие
, вычисленная в предположении, что событие 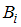 наступило.
наступило.
Событие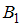 в данном случае состоит в том, что данные таблицы вводил первый программист. Тогда, согласно условию,
в данном случае состоит в том, что данные таблицы вводил первый программист. Тогда, согласно условию, 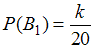 .
.
Событие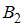 состоит в том, что с материалами работает второй программист. Так как события
состоит в том, что с материалами работает второй программист. Так как события 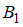 и
и 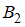 являются противоположными, то
являются противоположными, то 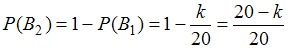 .
.
Так как вероятность ошибки ввода для первого программиста составляет 0,1, а для второго – 0,2, то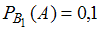 ,
, 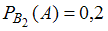 .
.
Рассчитаем вероятности событий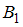 и
и 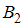 :
:
при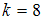 :
:
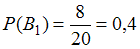 и
и 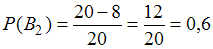 ;
;
при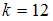 :
:
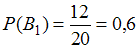 и
и 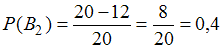 .
.
Подставив полученные значения в формулу полной вероятности, имеем
при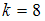 :
:
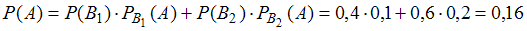 ;
;
при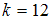 :
:
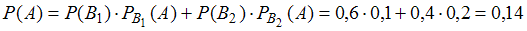 .
.
ответ тест i-exam
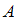 – случайно выбранная таблица содержит ошибку ввода. Оно может произойти при обработке данных как первым программистом (событие
– случайно выбранная таблица содержит ошибку ввода. Оно может произойти при обработке данных как первым программистом (событие 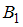 ), так и вторым (событие
), так и вторым (событие 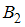 ). Заметим, что события
). Заметим, что события 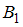 и
и 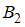 несовместны, поскольку с таблицей не могут работать два человека сразу, и противоположны, так как других вариантов для обработки материалов нет. Поэтому вероятность события
несовместны, поскольку с таблицей не могут работать два человека сразу, и противоположны, так как других вариантов для обработки материалов нет. Поэтому вероятность события 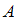 может быть определена при помощи формулы полной вероятности:
может быть определена при помощи формулы полной вероятности: 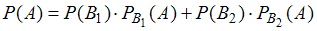 , где
, где 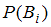 – вероятность события
– вероятность события 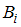 ;
; 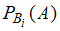 – условная вероятность события
– условная вероятность события 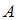 , то есть вероятность события
, то есть вероятность события 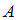 , вычисленная в предположении, что событие
, вычисленная в предположении, что событие 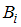 наступило.
наступило.Событие
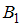 в данном случае состоит в том, что данные таблицы вводил первый программист. Тогда, согласно условию,
в данном случае состоит в том, что данные таблицы вводил первый программист. Тогда, согласно условию, 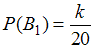 .
.Событие
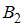 состоит в том, что с материалами работает второй программист. Так как события
состоит в том, что с материалами работает второй программист. Так как события 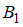 и
и 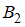 являются противоположными, то
являются противоположными, то 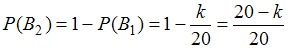 .
.Так как вероятность ошибки ввода для первого программиста составляет 0,1, а для второго – 0,2, то
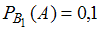 ,
, 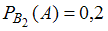 .
.Рассчитаем вероятности событий
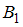 и
и 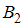 :
:при
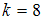 :
: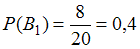 и
и 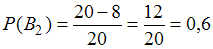 ;
;при
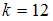 :
: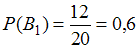 и
и 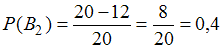 .
.Подставив полученные значения в формулу полной вероятности, имеем
при
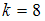 :
: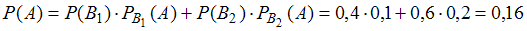 ;
;при
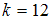 :
: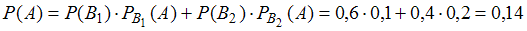 .
.ответ тест i-exam