Предмет:
Тема:
Формула полной вероятности и формула Бейеса
Вопрос:
Первый дефектоскоп проверяет 65% деталей (событие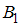 
), а второй – остальные (событие 
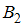). Вероятность того, что первый дефектоскоп не обнаружит брак, составляет 0,02; для второго дефектоскопа эта вероятность составляет 0,06.
Для расчета вероятности того, что случайно выбранная проверенная деталь оказалась бракованной (событие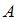 
), используется формула полной вероятности 
.
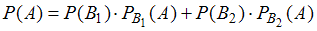Установите соответствие между обозначениями вероятностей и их числовыми значениями:
1). 
,
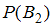2) 
,
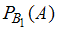3) 
.
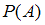Ответы:
1 0,35
2 0,02
3 0,034
0,06
Решение:
В задаче описывается событие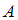 
– наличие брака в проверенной детали. Это событие может произойти как после проверки первым дефектоскопом (
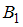), так и в результате сбоя второго дефектоскопа (
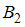), то есть событие 
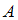совершается с одним из двух несовместных событий. Поэтому для расчета вероятности события 
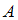используется формула полной вероятности: 
.
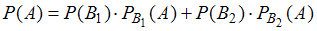Здесь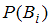
– вероятность события 
; 
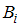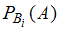– условная вероятность события 
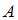, то есть вероятность события 
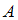, вычисленная в предположении, что событие 
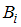наступило.
Событие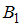
в данном случае состоит в том, что деталь была проверена первым дефектоскопом. Тогда, согласно условию, 
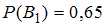. Так как события 
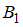и 
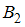являются противоположными, то 
.
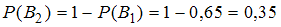Вероятность того, что случайно выбранная деталь, проверенная первым дефектоскопом, является бракованной, согласно условию, равна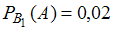
.
Вероятность того, что случайно выбранная деталь, проверенная вторым дефектоскопом, является бракованной, согласно условию, равна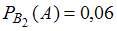
.
Подставив данные задачи в формулу, имеем: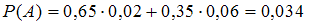
.
Следовательно,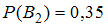
, 
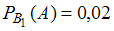и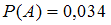 
.
ответ тест i-exam
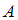– наличие брака в проверенной детали. Это событие может произойти как после проверки первым дефектоскопом (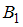), так и в результате сбоя второго дефектоскопа (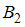), то есть событие 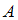совершается с одним из двух несовместных событий. Поэтому для расчета вероятности события 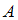используется формула полной вероятности: 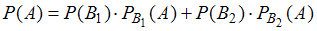.Здесь
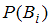– вероятность события 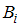; 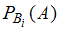– условная вероятность события 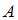, то есть вероятность события 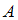, вычисленная в предположении, что событие 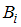наступило.Событие
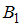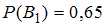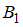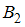в данном случае состоит в том, что деталь была проверена первым дефектоскопом. Тогда, согласно условию, . Так как события и являются противоположными, то 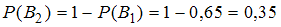. Вероятность того, что случайно выбранная деталь, проверенная первым дефектоскопом, является бракованной, согласно условию, равна
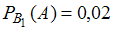.Вероятность того, что случайно выбранная деталь, проверенная вторым дефектоскопом, является бракованной, согласно условию, равна
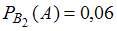.Подставив данные задачи в формулу, имеем:
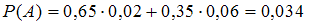.Следовательно,
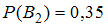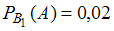, и 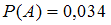.ответ тест i-exam
Похожие вопросы:
сила давления стержня CD на балку AB составляет 100 H. Для того чтобы балка AB сдвинулась, величина приложенной к ней горизонтальной силы должна равняться ___ H. (Результат округлить до целого значения.)
сила давления стержня CD на балку AB составляет 100 H. Для того чтобы балка AB сдвинулась, величина приложенной к ней горизонтальной силы должна равняться ___ H. (Результат округлить до целого значения.)
