Предмет:
Тема:
Декартово произведение множеств
Вопрос:
Известно, что декартовому произведению множеств 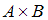 принадлежит пара
принадлежит пара 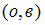 . Тогда множества A и B могут быть равны …
. Тогда множества A и B могут быть равны …
Ответы:
+ 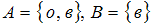
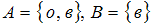
− 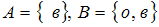
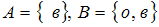
− 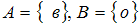
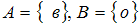
− 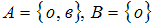
Решение:
Декартово произведение множеств 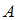 и
и 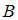 – это множество всех упорядоченных пар, первая компонента которых принадлежит множеству
– это множество всех упорядоченных пар, первая компонента которых принадлежит множеству 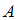 , а вторая – множеству
, а вторая – множеству 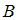 .
.
Так как по условию пара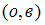 принадлежит декартовому произведению множеств
принадлежит декартовому произведению множеств 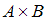 , то первая компонента пары
, то первая компонента пары 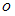 принадлежит множеству
принадлежит множеству 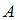 , а вторая компонента
, а вторая компонента 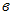 – множеству
– множеству 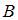 .
.
Если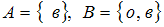 , то
, то 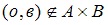 , так как
, так как 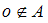 .
.
Если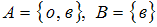 , то
, то 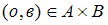 , так как
, так как 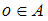 и
и 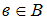 .
.
Если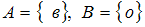 , то
, то 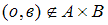 , так как
, так как 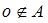 .
.
Если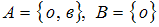 , то
, то 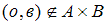 , так как
, так как 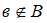 .
.
Таким образом, множества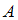 и
и 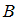 могут быть равны
могут быть равны 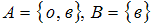 .
.
ответ тест i-exam
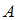 и
и 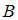 – это множество всех упорядоченных пар, первая компонента которых принадлежит множеству
– это множество всех упорядоченных пар, первая компонента которых принадлежит множеству 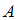 , а вторая – множеству
, а вторая – множеству 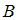 .
.Так как по условию пара
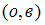 принадлежит декартовому произведению множеств
принадлежит декартовому произведению множеств 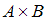 , то первая компонента пары
, то первая компонента пары 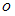 принадлежит множеству
принадлежит множеству 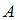 , а вторая компонента
, а вторая компонента 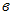 – множеству
– множеству 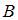 .
.Если
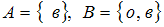 , то
, то 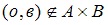 , так как
, так как 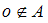 .
.Если
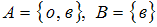 , то
, то 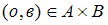 , так как
, так как 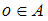 и
и 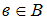 .
.Если
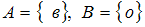 , то
, то 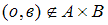 , так как
, так как 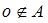 .
.Если
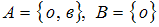 , то
, то 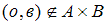 , так как
, так как 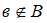 .
.Таким образом, множества
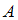 и
и 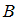 могут быть равны
могут быть равны 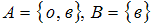 .
.ответ тест i-exam