Предмет:
Тема:
Формула полной вероятности и формула Бейеса
Вопрос:
В двух коробках по 10 яиц. В первой коробке 1 нестандартное яйцо, а во второй – 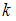 нестандартных яиц. При проверке наудачу берут одно яйцо из случайно выбранной коробки.
нестандартных яиц. При проверке наудачу берут одно яйцо из случайно выбранной коробки.
Установите соответствие между количеством нестандартных яиц во второй коробке и вероятностью того, что извлечено нестандартное яйцо:
1) 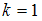 ,
,
2) 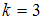 ,
,
3) 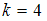 .
.
Ответы:
1 0,1
2 0,2
3 0,25
0,4
Решение:
Если событие 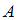 совершается с одним из
совершается с одним из 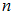 несовместных событий
несовместных событий 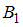 ,
, 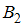 , …,
, …, 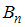 , то для определения вероятности этого события может быть использована формула полной вероятности
, то для определения вероятности этого события может быть использована формула полной вероятности
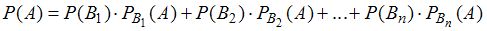 ,
,
где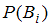 – вероятность события
– вероятность события 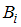 ;
; 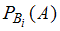 – условная вероятность события
– условная вероятность события 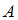 , то есть вероятность события
, то есть вероятность события 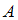 , вычисленная в предположении, что событие
, вычисленная в предположении, что событие 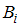 наступило.
наступило.
Событие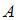 в данном случае состоит в том, что извлечено нестандартное яйцо. Оно может быть изъято либо из первой коробки (событие
в данном случае состоит в том, что извлечено нестандартное яйцо. Оно может быть изъято либо из первой коробки (событие 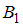 ), либо из второй (событие
), либо из второй (событие 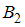 ).
).
Поскольку коробка выбирается наудачу, одна из двух, то вероятность того, что выбрана первая коробка,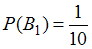 , вероятность того, что выбрана вторая,
, вероятность того, что выбрана вторая, 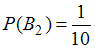 .
.
Условная вероятность того, что из первой коробки будет извлечено одно нестандартное яйцо,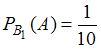 .
.
Условная вероятность того, что из второй коробки будет извлечено одно нестандартное яйцо,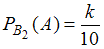 , где
, где 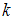 – количество нестандартных яиц во второй коробке.
– количество нестандартных яиц во второй коробке.
Подставив в формулу полной вероятности, имеем
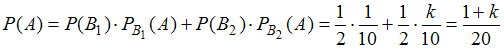 .
.
Вычислим значение вероятности события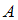 для разных значений
для разных значений 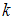 .
.
Если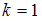 , то
, то 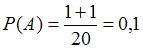 .
.
Если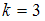 , то
, то 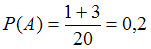 .
.
Если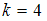 , то
, то 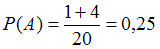 .
.
ответ тест i-exam
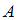 совершается с одним из
совершается с одним из 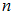 несовместных событий
несовместных событий 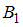 ,
, 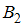 , …,
, …, 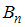 , то для определения вероятности этого события может быть использована формула полной вероятности
, то для определения вероятности этого события может быть использована формула полной вероятности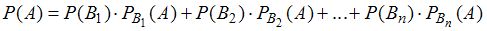 ,
,где
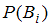 – вероятность события
– вероятность события 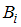 ;
; 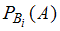 – условная вероятность события
– условная вероятность события 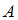 , то есть вероятность события
, то есть вероятность события 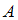 , вычисленная в предположении, что событие
, вычисленная в предположении, что событие 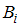 наступило.
наступило.Событие
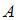 в данном случае состоит в том, что извлечено нестандартное яйцо. Оно может быть изъято либо из первой коробки (событие
в данном случае состоит в том, что извлечено нестандартное яйцо. Оно может быть изъято либо из первой коробки (событие 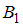 ), либо из второй (событие
), либо из второй (событие 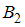 ).
).Поскольку коробка выбирается наудачу, одна из двух, то вероятность того, что выбрана первая коробка,
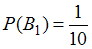 , вероятность того, что выбрана вторая,
, вероятность того, что выбрана вторая, 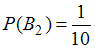 .
.Условная вероятность того, что из первой коробки будет извлечено одно нестандартное яйцо,
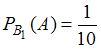 .
.Условная вероятность того, что из второй коробки будет извлечено одно нестандартное яйцо,
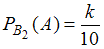 , где
, где 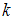 – количество нестандартных яиц во второй коробке.
– количество нестандартных яиц во второй коробке.Подставив в формулу полной вероятности, имеем
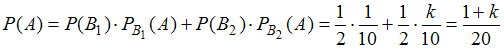 .
.Вычислим значение вероятности события
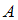 для разных значений
для разных значений 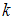 .
.Если
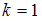 , то
, то 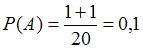 .
.Если
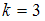 , то
, то 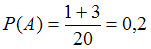 .
.Если
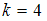 , то
, то 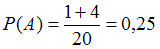 .
.ответ тест i-exam