Предмет:
Тема:
Элементы теории вероятностей. Математика случайного
Вопрос:
Произведено 50 подбрасываний игральной кости, при которых четное количество очков выпало 20 раз, а 5 очков – 5 раз. Событие 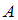 – «выпало четное количество очков», событие
– «выпало четное количество очков», событие 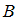 – «выпало 5 очков». Установите соответствие между относительными частотами указанных событий и их значениями:
– «выпало 5 очков». Установите соответствие между относительными частотами указанных событий и их значениями:
1) 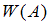 ,
,
2) 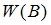 ,
,
3) 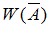 .
.
Ответы:
1 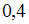
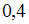
2 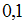
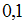
3 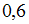
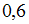
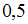
Решение:
Относительной частотой 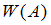 события
события 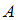 называется отношение числа опытов
называется отношение числа опытов 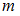 , в которых появилось это событие, к числу всех произведенных опытов
, в которых появилось это событие, к числу всех произведенных опытов 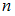 :
: 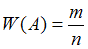 .
.
Событие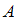 – «выпало четное количество очков» – произошло 20 раз в 50 опытах, т.е.
– «выпало четное количество очков» – произошло 20 раз в 50 опытах, т.е. 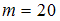 ,
, 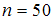 , поэтому
, поэтому 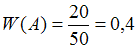 .
.
Событие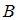 – «выпало 5 очков» – произошло 5 раз при 50 испытаниях, то есть
– «выпало 5 очков» – произошло 5 раз при 50 испытаниях, то есть 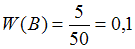 .
.
Событие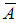 является противоположным для события
является противоположным для события 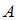 , то есть состоит в том, что в результате испытания событие
, то есть состоит в том, что в результате испытания событие 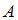 не произошло. «Выпадение нечетного количества очков» есть событие, противоположное событию
не произошло. «Выпадение нечетного количества очков» есть событие, противоположное событию 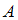 . Так как необходимо найти относительную частоту события
. Так как необходимо найти относительную частоту события 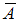 , противоположного
, противоположного 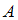 , то определим количество опытов, в которых данное событие
, то определим количество опытов, в которых данное событие 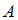 не произошло:
не произошло: 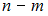 . Тогда
. Тогда 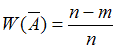 .
.
Событие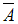 – «выпало нечетное количество очков» – происходит в тех случаях, когда не происходит событие
– «выпало нечетное количество очков» – происходит в тех случаях, когда не происходит событие 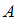 , поэтому число опытов, при которых событие
, поэтому число опытов, при которых событие 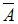 произошло, можно вычислить, вычитая из общего числа опытов количество опытов, когда произошли событие
произошло, можно вычислить, вычитая из общего числа опытов количество опытов, когда произошли событие 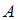 :
: 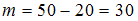 .
.
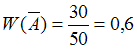 .
.
ответ тест i-exam
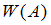 события
события 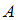 называется отношение числа опытов
называется отношение числа опытов 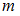 , в которых появилось это событие, к числу всех произведенных опытов
, в которых появилось это событие, к числу всех произведенных опытов 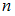 :
: 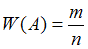 .
.Событие
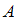 – «выпало четное количество очков» – произошло 20 раз в 50 опытах, т.е.
– «выпало четное количество очков» – произошло 20 раз в 50 опытах, т.е. 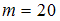 ,
, 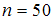 , поэтому
, поэтому 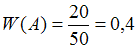 .
.Событие
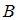 – «выпало 5 очков» – произошло 5 раз при 50 испытаниях, то есть
– «выпало 5 очков» – произошло 5 раз при 50 испытаниях, то есть 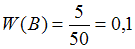 .
.Событие
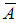 является противоположным для события
является противоположным для события 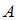 , то есть состоит в том, что в результате испытания событие
, то есть состоит в том, что в результате испытания событие 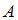 не произошло. «Выпадение нечетного количества очков» есть событие, противоположное событию
не произошло. «Выпадение нечетного количества очков» есть событие, противоположное событию 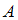 . Так как необходимо найти относительную частоту события
. Так как необходимо найти относительную частоту события 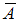 , противоположного
, противоположного 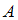 , то определим количество опытов, в которых данное событие
, то определим количество опытов, в которых данное событие 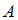 не произошло:
не произошло: 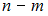 . Тогда
. Тогда 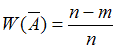 .
.Событие
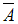 – «выпало нечетное количество очков» – происходит в тех случаях, когда не происходит событие
– «выпало нечетное количество очков» – происходит в тех случаях, когда не происходит событие 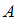 , поэтому число опытов, при которых событие
, поэтому число опытов, при которых событие 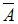 произошло, можно вычислить, вычитая из общего числа опытов количество опытов, когда произошли событие
произошло, можно вычислить, вычитая из общего числа опытов количество опытов, когда произошли событие 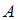 :
: 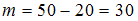 .
.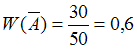 .
.ответ тест i-exam