Предмет:
Тема:
Характеристики вариационного ряда: мода и медиана
Вопрос:
Даны вариационные ряды: 2, 2, 2, 3, 4, 5, 5 и 3, 4, 4, 4, 6, 7, 8, 8. Сумма медиан этих рядов равна …
Ответы:
+ 8
− 7
− 9
− 6
Решение:
Медиана – это значение признака, приходящееся на середину вариационного ряда. Наблюдаемые значения рассматриваемого признака 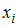 называются вариантами. Количество наблюдений данной варианты – частота
называются вариантами. Количество наблюдений данной варианты – частота 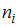 . Число объектов выборочной совокупности называется объемом выборки
. Число объектов выборочной совокупности называется объемом выборки 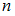 . Если объем выборки
. Если объем выборки 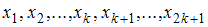 – нечетное число, то есть
– нечетное число, то есть 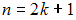 , то медианой является варианта
, то медианой является варианта 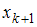 ; если объем выборки
; если объем выборки 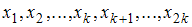 – четное число, то есть
– четное число, то есть 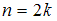 , медиана равна
, медиана равна 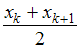 .
.
Объем выборки, представленной вариационным рядом 2, 2, 2, 3, 4, 5, 5, равен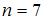 . Объем выборки – нечетное число, то есть
. Объем выборки – нечетное число, то есть 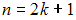 , отсюда
, отсюда 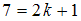 , то есть
, то есть  , а
, а 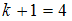 . Поэтому четвертый член ряда является его медианой. Варианта, имеющая номер 4,
. Поэтому четвертый член ряда является его медианой. Варианта, имеющая номер 4, 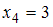 . Следовательно, медиана равна 3.
. Следовательно, медиана равна 3.
Объем выборки, представленной вариационным рядом 3, 4, 4, 4, 6, 7, 8, 8, равен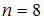 . Объем выборки – четное число, то есть
. Объем выборки – четное число, то есть 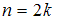 , отсюда
, отсюда 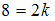 , то есть
, то есть 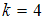 , а
, а 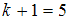 . Варианты, находящиеся в середине ряда, имеют номера 4 и 5 и равны
. Варианты, находящиеся в середине ряда, имеют номера 4 и 5 и равны 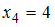 и
и 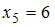 . Тогда медиана равна
. Тогда медиана равна 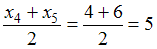 .
.
В итоге, сумма медиан равна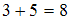 .
.
ответ тест i-exam
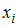 называются вариантами. Количество наблюдений данной варианты – частота
называются вариантами. Количество наблюдений данной варианты – частота 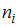 . Число объектов выборочной совокупности называется объемом выборки
. Число объектов выборочной совокупности называется объемом выборки 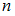 . Если объем выборки
. Если объем выборки 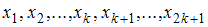 – нечетное число, то есть
– нечетное число, то есть 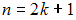 , то медианой является варианта
, то медианой является варианта 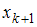 ; если объем выборки
; если объем выборки 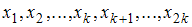 – четное число, то есть
– четное число, то есть 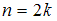 , медиана равна
, медиана равна 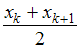 .
.Объем выборки, представленной вариационным рядом 2, 2, 2, 3, 4, 5, 5, равен
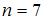 . Объем выборки – нечетное число, то есть
. Объем выборки – нечетное число, то есть 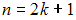 , отсюда
, отсюда 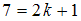 , то есть
, то есть  , а
, а 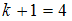 . Поэтому четвертый член ряда является его медианой. Варианта, имеющая номер 4,
. Поэтому четвертый член ряда является его медианой. Варианта, имеющая номер 4, 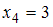 . Следовательно, медиана равна 3.
. Следовательно, медиана равна 3.Объем выборки, представленной вариационным рядом 3, 4, 4, 4, 6, 7, 8, 8, равен
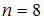 . Объем выборки – четное число, то есть
. Объем выборки – четное число, то есть 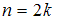 , отсюда
, отсюда 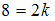 , то есть
, то есть 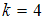 , а
, а 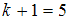 . Варианты, находящиеся в середине ряда, имеют номера 4 и 5 и равны
. Варианты, находящиеся в середине ряда, имеют номера 4 и 5 и равны 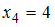 и
и 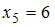 . Тогда медиана равна
. Тогда медиана равна 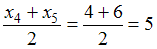 .
.В итоге, сумма медиан равна
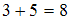 .
.ответ тест i-exam