Предмет:
Тема:
Формула полной вероятности и формула Бейеса
Вопрос:
Имеются три мерных стакана одинаковой формы. Вероятность ошибиться при измерении объема налитой жидкости более, чем на 2 мл, для первого мерного стакана составляет 0,2, для второго – 0,3, а для третьего – p. После проверки результатов измерения выбранным наудачу стаканом была обнаружена ошибка более, чем на 2 мл.
Установите соответствие между значениями p и вероятностью того, что измерение проводилось при помощи второго стакана:
Ответы:
1 0,5
2 0,3
0,1
Решение:
Для решения задачи необходимо воспользоваться формулой Бейеса. Пусть событие 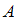 может наступить лишь при условии появления одного из
может наступить лишь при условии появления одного из 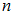 несовместных событий (гипотез)
несовместных событий (гипотез) 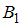 ,
, 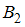 , …,
, …, 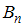 , образующих полную группу. Если событие
, образующих полную группу. Если событие 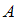 уже произошло, то вероятности гипотез могут быть переоценены по формулам Бейеса
уже произошло, то вероятности гипотез могут быть переоценены по формулам Бейеса
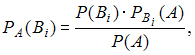
где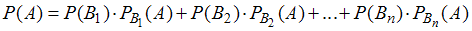 . В формуле использованы обозначения
. В формуле использованы обозначения 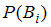 – вероятность события
– вероятность события 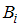 ;
; 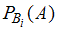 – условная вероятность события
– условная вероятность события 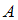 , то есть вероятность события
, то есть вероятность события 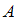 , вычисленная в предположении, что событие
, вычисленная в предположении, что событие 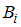 наступило.
наступило.
Событие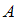 в данной задаче состоит в том, что измерение при помощи случайно выбранного стакана было ошибочным.
в данной задаче состоит в том, что измерение при помощи случайно выбранного стакана было ошибочным.
Гипотеза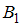 : измерение произведено при помощи первого стакана.
: измерение произведено при помощи первого стакана.
Гипотеза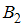 : измерение произведено при помощи второго стакана.
: измерение произведено при помощи второго стакана.
Гипотеза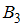 : измерение произведено при помощи третьего стакана.
: измерение произведено при помощи третьего стакана.
Искомые вероятности найдем по формуле Бейеса:
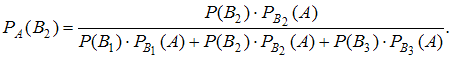
Все гипотезы равновозможны, поэтому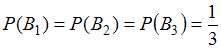 .
.
Из условия задачи имеем:
условная вероятность того, что при использовании первого стакана будет совершена ошибка более, чем на 2 мл, равна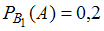 ;
;
условная вероятность того, что при использовании второго стакана будет совершена ошибка более, чем на 2 мл, равна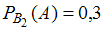 ;
;
условная вероятность того, что при использовании третьего стакана будет совершена ошибка более, чем на 2 мл, равна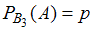 .
.
Подставив данные в формулу Бейеса, получим
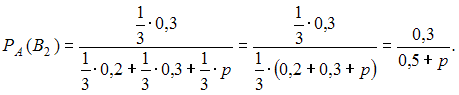
Вычислим для конкретного значения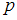 .
.
Если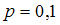 , то
, то 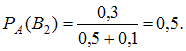
Если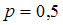 , то
, то 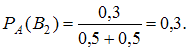
ответ тест i-exam
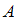 может наступить лишь при условии появления одного из
может наступить лишь при условии появления одного из 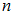 несовместных событий (гипотез)
несовместных событий (гипотез) 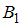 ,
, 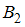 , …,
, …, 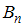 , образующих полную группу. Если событие
, образующих полную группу. Если событие 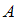 уже произошло, то вероятности гипотез могут быть переоценены по формулам Бейеса
уже произошло, то вероятности гипотез могут быть переоценены по формулам Бейеса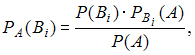
где
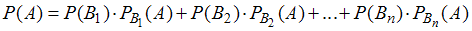 . В формуле использованы обозначения
. В формуле использованы обозначения 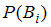 – вероятность события
– вероятность события 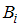 ;
; 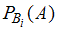 – условная вероятность события
– условная вероятность события 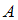 , то есть вероятность события
, то есть вероятность события 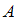 , вычисленная в предположении, что событие
, вычисленная в предположении, что событие 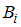 наступило.
наступило.Событие
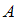 в данной задаче состоит в том, что измерение при помощи случайно выбранного стакана было ошибочным.
в данной задаче состоит в том, что измерение при помощи случайно выбранного стакана было ошибочным.Гипотеза
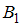 : измерение произведено при помощи первого стакана.
: измерение произведено при помощи первого стакана.Гипотеза
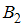 : измерение произведено при помощи второго стакана.
: измерение произведено при помощи второго стакана.Гипотеза
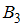 : измерение произведено при помощи третьего стакана.
: измерение произведено при помощи третьего стакана.Искомые вероятности найдем по формуле Бейеса:
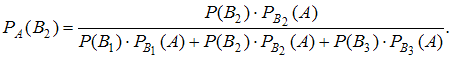
Все гипотезы равновозможны, поэтому
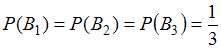 .
.Из условия задачи имеем:
условная вероятность того, что при использовании первого стакана будет совершена ошибка более, чем на 2 мл, равна
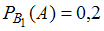 ;
;условная вероятность того, что при использовании второго стакана будет совершена ошибка более, чем на 2 мл, равна
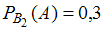 ;
;условная вероятность того, что при использовании третьего стакана будет совершена ошибка более, чем на 2 мл, равна
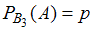 .
.Подставив данные в формулу Бейеса, получим
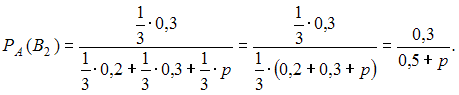
Вычислим для конкретного значения
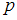 .
.Если
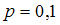 , то
, то 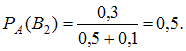
Если
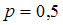 , то
, то 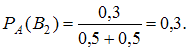
ответ тест i-exam