Предмет:
Тема:
Характеристики вариационного ряда: мода и медиана
Вопрос:
Дано статистическое распределение выборки
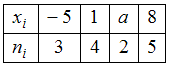
мода которого в 4 раза больше медианы. Тогда значение a равно …
Ответы:
+ 3
− 2
− 5
− 4
Решение:
Модой называется варианта, имеющая наибольшую частоту. Наблюдаемые значения рассматриваемого признака 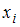 называются вариантами. Количество наблюдений данной варианты – это частота
называются вариантами. Количество наблюдений данной варианты – это частота 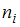 .
.
Статистическим распределением выборки называют перечень вариант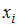 и соответствующих им частот
и соответствующих им частот 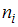 , который записывается в виде таблицы:
, который записывается в виде таблицы: 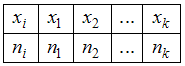
Согласно данному статистическому распределению
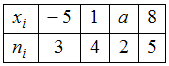
наибольшую частоту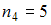 имеет варианта
имеет варианта 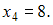 Значение моды, таким образом, равно 8.
Значение моды, таким образом, равно 8.
Так как мода в 4 раза больше медианы, то значение медианы равно 2.
Медиана – это значение признака, приходящееся на середину вариационного ряда. Наблюдаемые значения рассматриваемого признака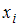 называются вариантами. Количество наблюдений данной варианты – частота
называются вариантами. Количество наблюдений данной варианты – частота 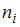 . Число объектов выборочной совокупности называется объемом выборки
. Число объектов выборочной совокупности называется объемом выборки 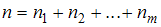 , где
, где 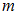 – количество вариант. Если объем
– количество вариант. Если объем 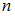 выборки
выборки 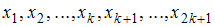 – нечетное число, то есть
– нечетное число, то есть 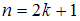 , то медианой является варианта
, то медианой является варианта 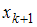 ; если объем
; если объем 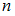 выборки
выборки 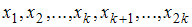 – четное число, то есть
– четное число, то есть 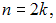 медиана равна
медиана равна 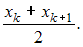
Объем данной выборки, представленной статистическим распределением,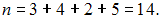 Это число четное, поэтому
Это число четное, поэтому 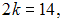 отсюда
отсюда 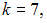 медиана равна
медиана равна 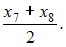
Из распределения
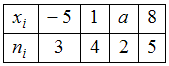
имеем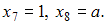 Согласно условию, медиана равна 2. Следовательно,
Согласно условию, медиана равна 2. Следовательно, 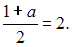 Отсюда имеем:
Отсюда имеем: 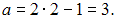
ответ тест i-exam
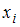 называются вариантами. Количество наблюдений данной варианты – это частота
называются вариантами. Количество наблюдений данной варианты – это частота 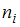 .
.Статистическим распределением выборки называют перечень вариант
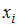 и соответствующих им частот
и соответствующих им частот 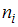 , который записывается в виде таблицы:
, который записывается в виде таблицы: 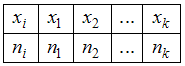
Согласно данному статистическому распределению
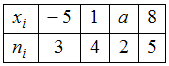
наибольшую частоту
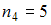 имеет варианта
имеет варианта 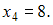 Значение моды, таким образом, равно 8.
Значение моды, таким образом, равно 8.Так как мода в 4 раза больше медианы, то значение медианы равно 2.
Медиана – это значение признака, приходящееся на середину вариационного ряда. Наблюдаемые значения рассматриваемого признака
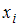 называются вариантами. Количество наблюдений данной варианты – частота
называются вариантами. Количество наблюдений данной варианты – частота 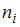 . Число объектов выборочной совокупности называется объемом выборки
. Число объектов выборочной совокупности называется объемом выборки 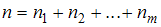 , где
, где 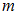 – количество вариант. Если объем
– количество вариант. Если объем 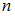 выборки
выборки 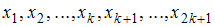 – нечетное число, то есть
– нечетное число, то есть 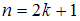 , то медианой является варианта
, то медианой является варианта 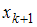 ; если объем
; если объем 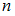 выборки
выборки 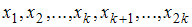 – четное число, то есть
– четное число, то есть 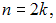 медиана равна
медиана равна 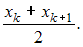
Объем данной выборки, представленной статистическим распределением,
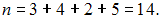 Это число четное, поэтому
Это число четное, поэтому 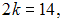 отсюда
отсюда 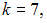 медиана равна
медиана равна 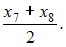
Из распределения
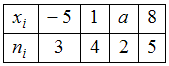
имеем
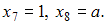 Согласно условию, медиана равна 2. Следовательно,
Согласно условию, медиана равна 2. Следовательно, 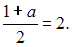 Отсюда имеем:
Отсюда имеем: 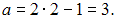
ответ тест i-exam