Предмет:
Тема:
Правило суммы и произведения
Вопрос:
Количество различных нечетных двузначных и трехзначных чисел, которые можно составить из цифр 1, 3, 6, 8, если в записи числа цифры могут повторяться, равно …
Ответы:
+40
Решение:
Если какой-либо объект можно выбрать 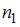 способами, второй объект –
способами, второй объект – 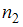 способами и так далее, а k-й объект –
способами и так далее, а k-й объект – 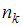 способами, то по правилу произведения
способами, то по правилу произведения 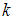 упорядоченных объектов можно выбрать
упорядоченных объектов можно выбрать 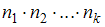 способами (правило произведения).
способами (правило произведения).
Если какой-либо объект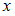 можно выбрать
можно выбрать 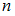 способами, а второй объект
способами, а второй объект 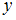 –
– 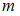 способами (не такими, как
способами (не такими, как 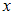 ), то объект
), то объект 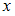 или
или 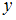 можно выбрать
можно выбрать 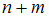 способами (правило суммы).
способами (правило суммы).
Нам необходимо подсчитать количество различных нечетных двузначных и трехзначных чисел, которые можно составить из цифр 1, 3, 6, 8, причем в записи числа цифры могут повторяться.
Двузначное число представляет собой упорядоченную пару цифр. Число нечетно, если оно оканчивается нечетной цифрой, значит, вторая цифра нашего числа может быть равна только 1 или 3, то есть может быть выбрана 2 способами. Так как цифры в числе могут повторяться, то первая его цифра может быть равна любой из данных цифр, то есть 1, 3, 6 или 8, значит, первую цифру мы можем выбрать 4 способами. Таким образом, количество искомых двузначных чисел по правилу произведения будет равно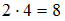 .
.
Трехзначное число представляет собой упорядоченную тройку цифр. Так как число нечетное, то цифру, которой оно оканчивается, можно выбрать 2 способами, а первую и вторую цифру можно выбрать 4 способами. Таким образом, количество искомых трехзначных чисел по правилу произведения будет равно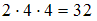 .
.
Таким образом, количество искомых двузначных и трехзначных чисел по правилу суммы будет равно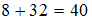 .
.
ответ тест i-exam
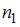 способами, второй объект –
способами, второй объект – 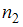 способами и так далее, а k-й объект –
способами и так далее, а k-й объект – 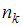 способами, то по правилу произведения
способами, то по правилу произведения 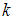 упорядоченных объектов можно выбрать
упорядоченных объектов можно выбрать 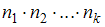 способами (правило произведения).
способами (правило произведения).Если какой-либо объект
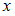 можно выбрать
можно выбрать 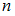 способами, а второй объект
способами, а второй объект 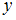 –
– 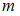 способами (не такими, как
способами (не такими, как 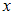 ), то объект
), то объект 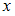 или
или 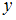 можно выбрать
можно выбрать 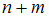 способами (правило суммы).
способами (правило суммы).Нам необходимо подсчитать количество различных нечетных двузначных и трехзначных чисел, которые можно составить из цифр 1, 3, 6, 8, причем в записи числа цифры могут повторяться.
Двузначное число представляет собой упорядоченную пару цифр. Число нечетно, если оно оканчивается нечетной цифрой, значит, вторая цифра нашего числа может быть равна только 1 или 3, то есть может быть выбрана 2 способами. Так как цифры в числе могут повторяться, то первая его цифра может быть равна любой из данных цифр, то есть 1, 3, 6 или 8, значит, первую цифру мы можем выбрать 4 способами. Таким образом, количество искомых двузначных чисел по правилу произведения будет равно
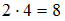 .
.Трехзначное число представляет собой упорядоченную тройку цифр. Так как число нечетное, то цифру, которой оно оканчивается, можно выбрать 2 способами, а первую и вторую цифру можно выбрать 4 способами. Таким образом, количество искомых трехзначных чисел по правилу произведения будет равно
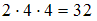 .
.Таким образом, количество искомых двузначных и трехзначных чисел по правилу суммы будет равно
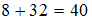 .
.ответ тест i-exam