Предмет:
Тема:
Точечные оценки параметров распределения
Вопрос:
Выборочная средняя выборки, полигон относительных частот которой задан на рисунке
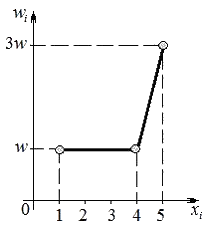
равна 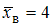 . Тогда выборочная дисперсия равна …
. Тогда выборочная дисперсия равна …
Ответы:
+ 2,4
− 2,6
− 1,8
− 0
Решение:
Для расчета выборочной дисперсии воспользуемся формулой: 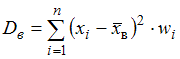 . Вспомним смысл статистических понятий, входящих в состав данной формулы.
. Вспомним смысл статистических понятий, входящих в состав данной формулы.
Согласно условию,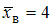 .
. 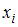 – наблюдаемые значения рассматриваемого признака, которые называются вариантами. Количество наблюдений данной варианты – частота
– наблюдаемые значения рассматриваемого признака, которые называются вариантами. Количество наблюдений данной варианты – частота 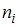 . Отношения числа наблюдений к объему выборки
. Отношения числа наблюдений к объему выборки 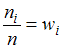 называют относительными частотами.
называют относительными частотами.
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки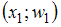 ,
, 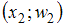 , …,
, …, 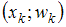 . По полигону относительных частот находим координаты точек:
. По полигону относительных частот находим координаты точек: 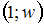 ;
; 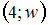 ,
, 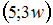 .
.
Найдем значение неизвестной относительной частоты из соотношения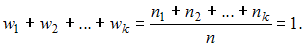 Имеем
Имеем 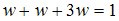 , откуда
, откуда 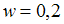 ;
; 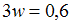 .
.
Таким образом, имеем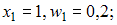
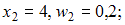
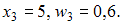
Находим выборочную дисперсию:
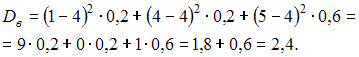
ответ тест i-exam
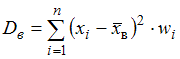 . Вспомним смысл статистических понятий, входящих в состав данной формулы.
. Вспомним смысл статистических понятий, входящих в состав данной формулы.Согласно условию,
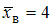 .
. 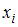 – наблюдаемые значения рассматриваемого признака, которые называются вариантами. Количество наблюдений данной варианты – частота
– наблюдаемые значения рассматриваемого признака, которые называются вариантами. Количество наблюдений данной варианты – частота 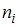 . Отношения числа наблюдений к объему выборки
. Отношения числа наблюдений к объему выборки 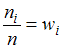 называют относительными частотами.
называют относительными частотами.Полигоном относительных частот называют ломаную, отрезки которой соединяют точки
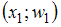 ,
, 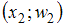 , …,
, …, 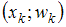 . По полигону относительных частот находим координаты точек:
. По полигону относительных частот находим координаты точек: 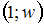 ;
; 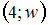 ,
, 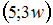 .
.Найдем значение неизвестной относительной частоты из соотношения
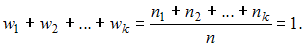 Имеем
Имеем 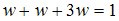 , откуда
, откуда 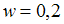 ;
; 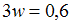 .
.Таким образом, имеем
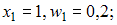
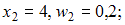
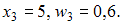
Находим выборочную дисперсию:
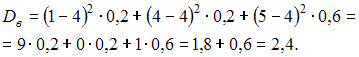
ответ тест i-exam