Предмет:
Тема:
Характеристики вариационного ряда: мода и медиана
Вопрос:
Статическое распределение выборки с модой, равной 4, имеет вид:
Ответы:
+ 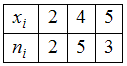
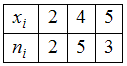
− 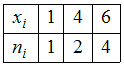
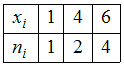
− 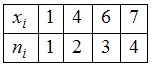
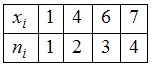
− 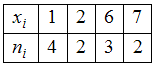
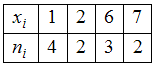
Решение:
Модой называется варианта, имеющая наибольшую частоту. Наблюдаемые значения рассматриваемого признака 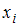 называются вариантами. Количество наблюдений данной варианты – это частота
называются вариантами. Количество наблюдений данной варианты – это частота 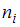 .
.
Для статистического распределения
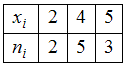
в соответствующем вариационном ряде варианта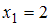 появилась с частотой
появилась с частотой 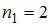 , варианта
, варианта 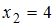 – с частотой
– с частотой 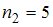 , а варианта
, а варианта 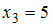 – с частотой
– с частотой 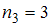 . Наибольшую частоту имеет варианта
. Наибольшую частоту имеет варианта 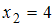 , она и является модой.
, она и является модой.
Для статистического распределения
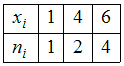
в соответствующем вариационном ряде варианта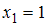 появилась с частотой
появилась с частотой 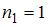 , варианта
, варианта 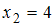 – с частотой
– с частотой 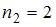 , а варианта
, а варианта 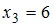 – с частотой
– с частотой 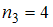 . Наибольшую частоту имеет варианта
. Наибольшую частоту имеет варианта  , поэтому мода равна 6.
, поэтому мода равна 6.
Для статистического распределения
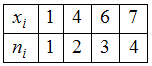
в соответствующем вариационном ряде варианта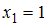 появилась с частотой
появилась с частотой 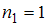 , варианта
, варианта 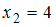 – с частотой
– с частотой 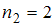 , варианта
, варианта 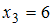 – с частотой
– с частотой 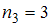 , а варианта
, а варианта 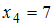 – с частотой
– с частотой 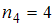 . Наибольшую частоту имеет варианта
. Наибольшую частоту имеет варианта 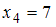 , поэтому мода равна 7.
, поэтому мода равна 7.
Для статистического распределения
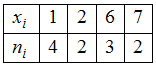
в соответствующем вариационном ряде варианта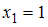 появилась с частотой
появилась с частотой 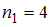 , варианта
, варианта 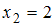 – с частотой
– с частотой 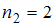 , варианта
, варианта 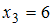 – с частотой
– с частотой 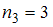 , а варианта
, а варианта 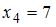 – с частотой
– с частотой 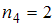 . Наибольшую частоту имеет варианта
. Наибольшую частоту имеет варианта 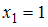 , поэтому мода равна 1.
, поэтому мода равна 1.
Следовательно, статистическое распределение выборки с модой, равной 4, имеет вид:
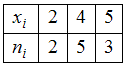 .
.
ответ тест i-exam
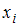 называются вариантами. Количество наблюдений данной варианты – это частота
называются вариантами. Количество наблюдений данной варианты – это частота 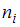 .
.Для статистического распределения
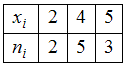
в соответствующем вариационном ряде варианта
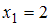 появилась с частотой
появилась с частотой 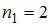 , варианта
, варианта 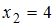 – с частотой
– с частотой 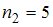 , а варианта
, а варианта 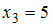 – с частотой
– с частотой 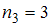 . Наибольшую частоту имеет варианта
. Наибольшую частоту имеет варианта 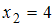 , она и является модой.
, она и является модой.Для статистического распределения
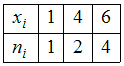
в соответствующем вариационном ряде варианта
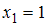 появилась с частотой
появилась с частотой 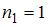 , варианта
, варианта 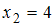 – с частотой
– с частотой 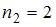 , а варианта
, а варианта 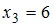 – с частотой
– с частотой 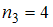 . Наибольшую частоту имеет варианта
. Наибольшую частоту имеет варианта  , поэтому мода равна 6.
, поэтому мода равна 6.Для статистического распределения
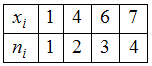
в соответствующем вариационном ряде варианта
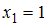 появилась с частотой
появилась с частотой 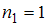 , варианта
, варианта 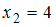 – с частотой
– с частотой 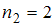 , варианта
, варианта 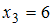 – с частотой
– с частотой 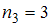 , а варианта
, а варианта 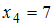 – с частотой
– с частотой 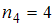 . Наибольшую частоту имеет варианта
. Наибольшую частоту имеет варианта 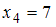 , поэтому мода равна 7.
, поэтому мода равна 7.Для статистического распределения
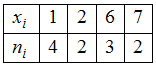
в соответствующем вариационном ряде варианта
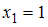 появилась с частотой
появилась с частотой 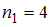 , варианта
, варианта 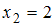 – с частотой
– с частотой 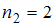 , варианта
, варианта 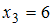 – с частотой
– с частотой 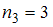 , а варианта
, а варианта 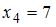 – с частотой
– с частотой 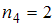 . Наибольшую частоту имеет варианта
. Наибольшую частоту имеет варианта 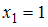 , поэтому мода равна 1.
, поэтому мода равна 1.Следовательно, статистическое распределение выборки с модой, равной 4, имеет вид:
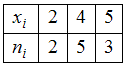 .
.ответ тест i-exam