Предмет:
Тема:
Проверка статистических гипотез
Вопрос:
По двум независимым выборкам, объемы которых 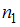 ,
, 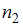 , извлеченным из нормальных совокупностей
, извлеченным из нормальных совокупностей 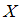 и
и 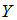 , найдены исправленные выборочные дисперсии
, найдены исправленные выборочные дисперсии 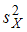 и
и 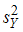 . Надо проверить нулевую гипотезу
. Надо проверить нулевую гипотезу 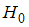 :
: 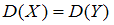 о равенстве генеральных дисперсий, при конкурирующей гипотезе
о равенстве генеральных дисперсий, при конкурирующей гипотезе 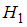 :
: 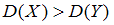 . Для этого надо вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей)
. Для этого надо вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей) 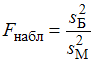 и сравнить с критической точкой
и сравнить с критической точкой 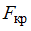 . Если
. Если 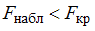 – нет основания отвергнуть нулевую гипотезу. Если
– нет основания отвергнуть нулевую гипотезу. Если 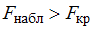 – нулевую гипотезу отвергают.
– нулевую гипотезу отвергают.
Известно, что 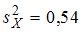 и
и 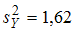 . Тогда значение критической точки
. Тогда значение критической точки 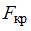 , при котором нулевую гипотезу принимают, равно …
, при котором нулевую гипотезу принимают, равно …
Ответы:
+ 3,25
− 1,2
− 2,7
− 0,82
Решение:
По условию задачи, для того чтобы проверить нулевую гипотезу 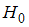 :
: 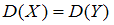 о равенстве генеральных дисперсий, при конкурирующей гипотезе
о равенстве генеральных дисперсий, при конкурирующей гипотезе 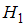 :
: 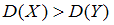 , надо вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей)
, надо вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей) 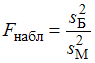 и сравнить с критической точкой
и сравнить с критической точкой 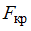 . Если
. Если 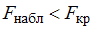 – нет основания отвергнуть нулевую гипотезу. Если
– нет основания отвергнуть нулевую гипотезу. Если 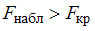 – нулевую гипотезу отвергают.
– нулевую гипотезу отвергают.
Вычислим наблюдаемое значение критерия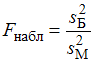 и сравним со значением критической точки
и сравним со значением критической точки 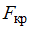 . Поскольку
. Поскольку 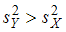 , то получим
, то получим 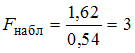 . Сравним с данными значениями критической точки. Только для
. Сравним с данными значениями критической точки. Только для 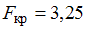 получаем, что
получаем, что 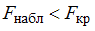 , и нулевую гипотезу принимают.
, и нулевую гипотезу принимают.
Следовательно, значение критической точки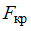 , при котором нулевую гипотезу принимают, равно 3,25.
, при котором нулевую гипотезу принимают, равно 3,25.
ответ тест i-exam
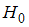 :
: 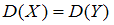 о равенстве генеральных дисперсий, при конкурирующей гипотезе
о равенстве генеральных дисперсий, при конкурирующей гипотезе 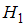 :
: 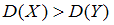 , надо вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей)
, надо вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей) 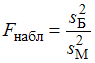 и сравнить с критической точкой
и сравнить с критической точкой 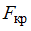 . Если
. Если 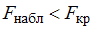 – нет основания отвергнуть нулевую гипотезу. Если
– нет основания отвергнуть нулевую гипотезу. Если 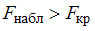 – нулевую гипотезу отвергают.
– нулевую гипотезу отвергают.Вычислим наблюдаемое значение критерия
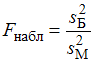 и сравним со значением критической точки
и сравним со значением критической точки 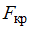 . Поскольку
. Поскольку 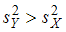 , то получим
, то получим 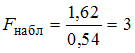 . Сравним с данными значениями критической точки. Только для
. Сравним с данными значениями критической точки. Только для 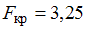 получаем, что
получаем, что 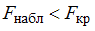 , и нулевую гипотезу принимают.
, и нулевую гипотезу принимают.Следовательно, значение критической точки
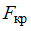 , при котором нулевую гипотезу принимают, равно 3,25.
, при котором нулевую гипотезу принимают, равно 3,25.ответ тест i-exam