Предмет:
Тема:
Интервальные оценки параметров распределения
Вопрос:
Для оценки с надежностью 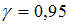 математического ожидания
математического ожидания 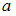 нормально распределенного признака
нормально распределенного признака 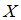 по выборочной средней
по выборочной средней 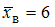 при среднем квадратичном отклонении
при среднем квадратичном отклонении 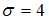 генеральной совокупности использовали доверительный интервал
генеральной совокупности использовали доверительный интервал 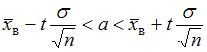 , где
, где 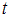 – значение аргумента функции Лапласа
– значение аргумента функции Лапласа 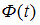 , при котором
, при котором 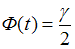 ,
, 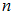 – объем выборки. Значение аргумента функции Лапласа для
– объем выборки. Значение аргумента функции Лапласа для 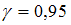 равно
равно 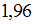 .
.
Установите соответствие между доверительными интервалами и объемами выборки 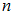 .
.
1. 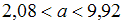
2. 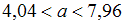
Ответы:
1 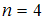
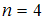
2 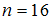
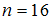
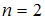
Решение:
Доверительный интервал определяется формулой 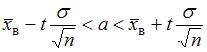 . Знание значений границ интервала дает возможность найти объем выборки.
. Знание значений границ интервала дает возможность найти объем выборки.
Рассмотрим первый интервал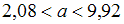 . Используя левую границу интервала, можно записать
. Используя левую границу интервала, можно записать 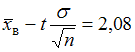 . По условию задачи известно, что
. По условию задачи известно, что 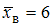 ,
, 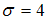 и
и 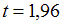 . Тогда
. Тогда 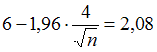 . Откуда
. Откуда 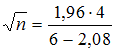 . Следовательно,
. Следовательно, 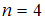 .
.
Аналогично, рассмотрим интервал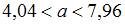 . Тогда имеем
. Тогда имеем 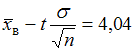 . Подставив данные из условия задачи, получим
. Подставив данные из условия задачи, получим 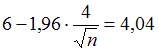 . Откуда
. Откуда 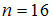 .
.
Следовательно, доверительному интервалу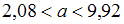 соответствует выборка объемом 4, а интервал
соответствует выборка объемом 4, а интервал 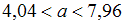 вычислен для выборки объемом 16.
вычислен для выборки объемом 16.
ответ тест i-exam
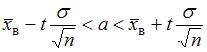 . Знание значений границ интервала дает возможность найти объем выборки.
. Знание значений границ интервала дает возможность найти объем выборки.Рассмотрим первый интервал
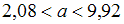 . Используя левую границу интервала, можно записать
. Используя левую границу интервала, можно записать 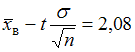 . По условию задачи известно, что
. По условию задачи известно, что 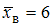 ,
, 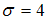 и
и 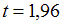 . Тогда
. Тогда 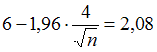 . Откуда
. Откуда 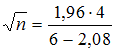 . Следовательно,
. Следовательно, 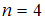 .
. Аналогично, рассмотрим интервал
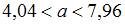 . Тогда имеем
. Тогда имеем 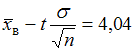 . Подставив данные из условия задачи, получим
. Подставив данные из условия задачи, получим 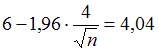 . Откуда
. Откуда 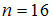 .
.Следовательно, доверительному интервалу
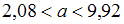 соответствует выборка объемом 4, а интервал
соответствует выборка объемом 4, а интервал 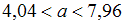 вычислен для выборки объемом 16.
вычислен для выборки объемом 16.ответ тест i-exam