Предмет:
Тема:
Интервальные оценки параметров распределения
Вопрос:
Дан доверительный интервал (20,2; 25,4) для оценки математического ожидания нормально распределенного количественного признака при известном среднем квадратическом отклонении генеральной совокупности. Тогда при увеличении объема выборки в четыре раза этот доверительный интервал примет вид …
Ответы:
+ (21,5; 24,1)
− (17,6; 28,0)
− (21,45; 24,15)
− (12,0; 33,6)
Решение:
Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде симметричного интервала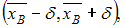 
где 
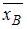– точечная оценка математического ожидания, 
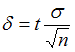– точность оценки, 
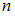– объем выборки, 
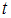– значение аргумента функции Лапласа Ф(t), при котором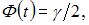 
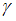– надежность оценки.
Для данной интервальной оценки вычислим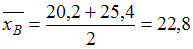
и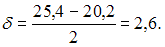 
В случае увеличения объема выборки в четыре раза значение точности оценки уменьшится в 
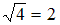раза, то есть значение 
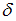будет равно 1,3.
Тогда интервальная оценка примет вид (22,8 – 1,3; 22,8 + 1,3), или (21,5; 24,1).
ответ тест i-exam
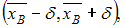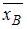где – точечная оценка математического ожидания, 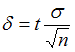– точность оценки, 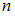– объем выборки, 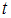– значение аргумента функции Лапласа Ф(t), при котором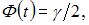 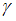– надежность оценки. Для данной интервальной оценки вычислим
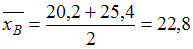и 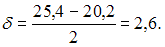В случае увеличения объема выборки в четыре раза значение точности оценки уменьшится в 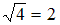раза, то есть значение 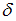будет равно 1,3.Тогда интервальная оценка примет вид (22,8 – 1,3; 22,8 + 1,3), или (21,5; 24,1).
ответ тест i-exam