Ответы:
+ 2
− – 1
− 3
− 0
Решение:
Данная функция определена и непрерывна на каждом из интервалов 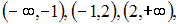 и меняет свое аналитическое выражение в точках
и меняет свое аналитическое выражение в точках 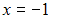 и
и 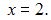 Поэтому функция может иметь разрыв только в этих точках. Исследуем их на непрерывность.
Поэтому функция может иметь разрыв только в этих точках. Исследуем их на непрерывность.
Для точки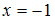 вычислим односторонние пределы и значение функции в этой точке:
вычислим односторонние пределы и значение функции в этой точке:
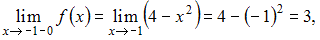
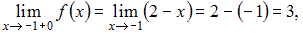 и
и 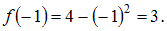
Так как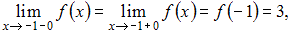 то точка
то точка 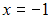 является точкой непрерывности данной функции.
является точкой непрерывности данной функции.
Для точки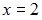 вычислим односторонние пределы и значение функции в этой точке:
вычислим односторонние пределы и значение функции в этой точке:
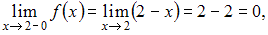
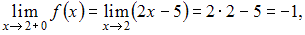 и
и 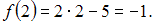
Так как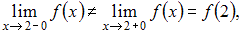 то точка
то точка 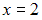 является точкой разрыва первого рода.
является точкой разрыва первого рода.
ответ тест i-exam
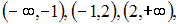 и меняет свое аналитическое выражение в точках
и меняет свое аналитическое выражение в точках 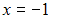 и
и 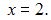 Поэтому функция может иметь разрыв только в этих точках. Исследуем их на непрерывность.
Поэтому функция может иметь разрыв только в этих точках. Исследуем их на непрерывность.Для точки
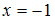 вычислим односторонние пределы и значение функции в этой точке:
вычислим односторонние пределы и значение функции в этой точке: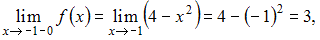
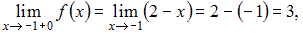 и
и 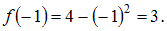
Так как
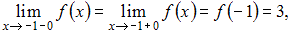 то точка
то точка 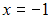 является точкой непрерывности данной функции.
является точкой непрерывности данной функции.Для точки
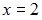 вычислим односторонние пределы и значение функции в этой точке:
вычислим односторонние пределы и значение функции в этой точке: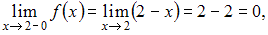
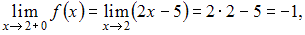 и
и 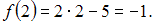
Так как
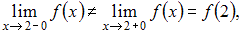 то точка
то точка 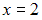 является точкой разрыва первого рода.
является точкой разрыва первого рода.ответ тест i-exam
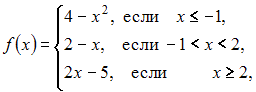 равна …
равна …