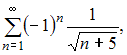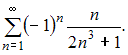Ответы:
+ ряд А) сходится условно, ряд В) сходится абсолютно
− ряд А) сходится условно, ряд В) сходится условно
− ряд А) расходится, ряд В) сходится абсолютно
− ряд А) расходится, ряд В) сходится условно
Решение:
Для исследования сходимости знакочередующегося ряда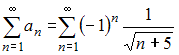 
применим признак сходимости Лейбница.
Тогда:
1) вычислим предел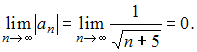
2) для любого натурального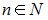
справедливо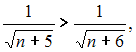 
то есть последовательность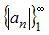
монотонно убывает.
Следовательно, ряд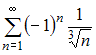
сходится.
Теперь проверим ряд на абсолютную сходимость. Для этого составим знакоположительный числовой ряд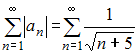
и исследуем его сходимость по теореме сравнения с расходящимся обобщенным гармоническим рядом 
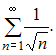Тогда 
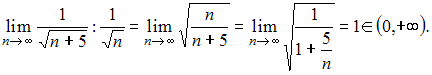
То есть ряд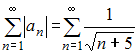
расходится, следовательно, ряд 
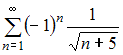сходится условно.
Теперь исследуем на сходимость ряд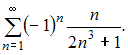
Этот ряд сходится абсолютно, так как при применении теоремы сравнения со сходящимся обобщенным гармоническим рядом 
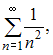получаем:
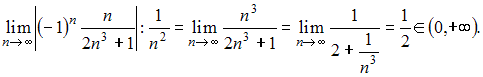
А это означает, что ряд
сходится.
ответ тест i-exam
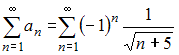применим признак сходимости Лейбница. Тогда:
1) вычислим предел
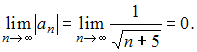
2) для любого натурального
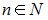справедливо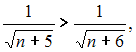 то есть последовательность
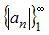монотонно убывает.Следовательно, ряд
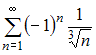сходится.Теперь проверим ряд на абсолютную сходимость. Для этого составим знакоположительный числовой ряд
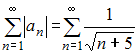и исследуем его сходимость по теореме сравнения с расходящимся обобщенным гармоническим рядом 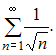Тогда 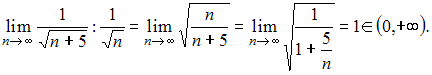То есть ряд
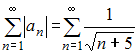расходится, следовательно, ряд 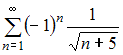сходится условно.Теперь исследуем на сходимость ряд
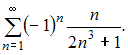Этот ряд сходится абсолютно, так как при применении теоремы сравнения со сходящимся обобщенным гармоническим рядом 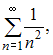получаем: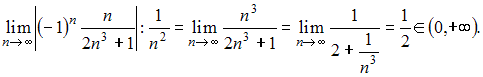 А это означает, что ряд
сходится.ответ тест i-exam