Предмет:
Тема:
Линейное программирование: аналитическое задание области допустимых решений
Вопрос:
Дана задача линейного программирования: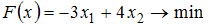 
, при ограничениях:
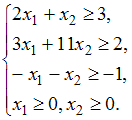
Тогда симметричная ей двойственная задача линейного программирования будет иметь вид …
Ответы:
+ 
− 
− 
− 
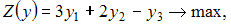
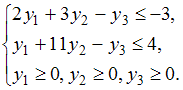
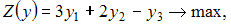
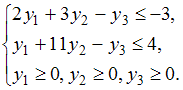
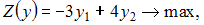
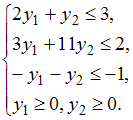
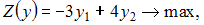
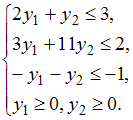
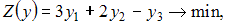
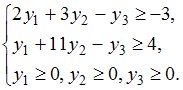
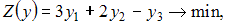
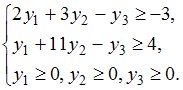
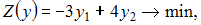
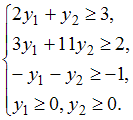
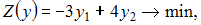
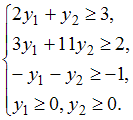
Решение:
Симметричная двойственная задача составляется для нахождения максимума функции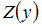 
, количество переменных в которой равно числу неравенств системы ограничений прямой задачи. Следовательно, их будет 3: y1, y2, y3. Все ограничения двойственной задачи будут вида «
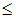». Коэффициенты при переменных целевой функции одной задачи являются свободными членами системы ограничений другой. Матрицы коэффициентов при переменных являются транспонированными друг к другу. Переменные y1, y2, y3 должны быть неотрицательными. Тогда симметричная двойственная задача линейного программирования будет иметь вид:
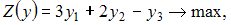
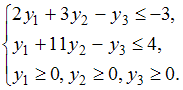
ответ тест i-exam
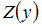, количество переменных в которой равно числу неравенств системы ограничений прямой задачи. Следовательно, их будет 3: y1, y2, y3. Все ограничения двойственной задачи будут вида «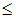». Коэффициенты при переменных целевой функции одной задачи являются свободными членами системы ограничений другой. Матрицы коэффициентов при переменных являются транспонированными друг к другу. Переменные y1, y2, y3 должны быть неотрицательными. 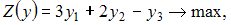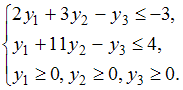Тогда симметричная двойственная задача линейного программирования будет иметь вид:ответ тест i-exam