Предмет:
Тема:
Дифференциальные уравнения высших порядков, допускающие понижение порядка
Вопрос:
Уравнение кривой, радиус кривизны которой равен кубу нормали имеет вид …
Ответы:
+ 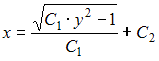
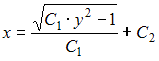
− 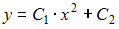
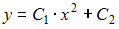
− 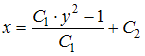
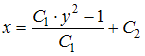
− 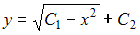
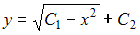
Решение:
Радиус кривизны плоской кривой выражается формулой 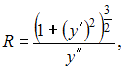
а длина нормали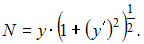 Тогда для нахождения уравнения искомой кривой получим уравнение
Тогда для нахождения уравнения искомой кривой получим уравнение 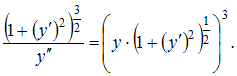 Сократив на
Сократив на 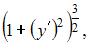 получим уравнение
получим уравнение 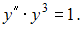
Так как уравнение не содержит в явном виде аргумент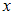 , то применима замена
, то применима замена 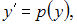 тогда
тогда 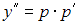 и данное дифференциальное уравнение примет вид
и данное дифференциальное уравнение примет вид 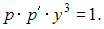 Это уравнение первого порядка относительно функции
Это уравнение первого порядка относительно функции 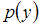 с разделяющимися переменными.
с разделяющимися переменными.
Решим его: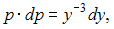
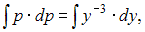
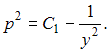 Возвращаясь к переменной
Возвращаясь к переменной 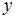 , приходим к уравнению
, приходим к уравнению 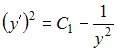 или
или 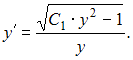
Разделив переменные и проинтегрировав обе части, получим: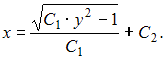
ответ тест i-exam
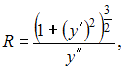
а длина нормали
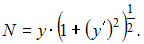 Тогда для нахождения уравнения искомой кривой получим уравнение
Тогда для нахождения уравнения искомой кривой получим уравнение 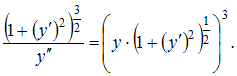 Сократив на
Сократив на 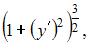 получим уравнение
получим уравнение 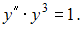
Так как уравнение не содержит в явном виде аргумент
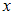 , то применима замена
, то применима замена 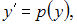 тогда
тогда 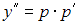 и данное дифференциальное уравнение примет вид
и данное дифференциальное уравнение примет вид 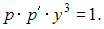 Это уравнение первого порядка относительно функции
Это уравнение первого порядка относительно функции 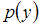 с разделяющимися переменными.
с разделяющимися переменными. Решим его:
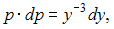
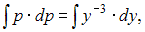
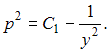 Возвращаясь к переменной
Возвращаясь к переменной 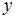 , приходим к уравнению
, приходим к уравнению 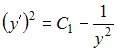 или
или 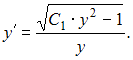
Разделив переменные и проинтегрировав обе части, получим:
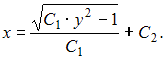
ответ тест i-exam