Предмет:
Тема:
Однородные дифференциальные уравнения
Вопрос:
Общий интеграл дифференциального уравнения 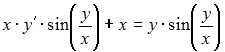 имеет вид …
имеет вид …
Ответы:
+ 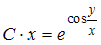 , где
, где 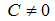
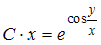 , где
, где 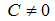
− 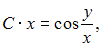 где
где 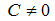
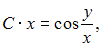 где
где 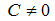
− 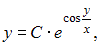 где
где 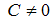
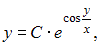 где
где 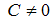
− 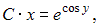 где
где 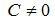
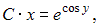 где
где 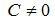
Решение:
Сделаем замену 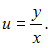 Тогда
Тогда 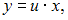
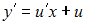 и уравнение
и уравнение 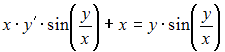 примет вид:
примет вид: 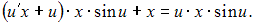 После преобразований получим уравнение с разделяющимися переменными
После преобразований получим уравнение с разделяющимися переменными 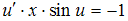
или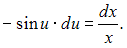 Проинтегрировав обе части, получим:
Проинтегрировав обе части, получим: 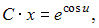 где
где 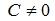 . Сделаем обратную замену:
. Сделаем обратную замену: 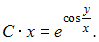
ответ тест i-exam
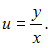 Тогда
Тогда 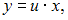
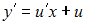 и уравнение
и уравнение 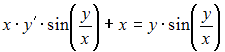 примет вид:
примет вид: 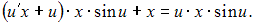 После преобразований получим уравнение с разделяющимися переменными
После преобразований получим уравнение с разделяющимися переменными 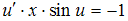
или
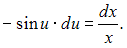 Проинтегрировав обе части, получим:
Проинтегрировав обе части, получим: 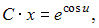 где
где 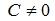 . Сделаем обратную замену:
. Сделаем обратную замену: 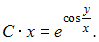
ответ тест i-exam