Предмет:
Тема:
Дифференциальные уравнения высших порядков, допускающие понижение порядка
Вопрос:
Общее решение дифференциального уравнения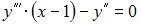 
при 
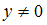имеет вид …
Ответы:
+ 
− 
− 
− 
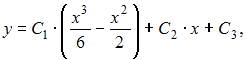
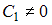
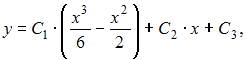
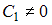
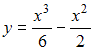
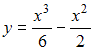
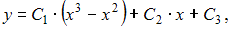
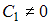
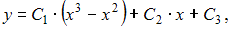
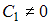
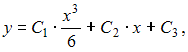
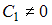
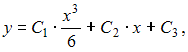
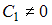
Решение:
Для решения дифференциального уравнения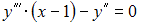 
необходимо сделать замену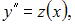 
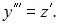Тогда порядок этого уравнения понизится на две единицы и оно примет вид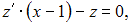 
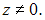
Это уравнение первого порядка с разделяющимися переменными. Разделив переменные, получим: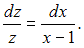
Тогда 
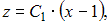где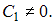 
Сделав обратную замену, получим дифференциальное уравнение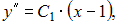 
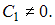
Проинтегрируем последовательно обе части уравнения два раза: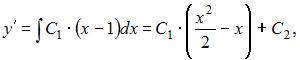
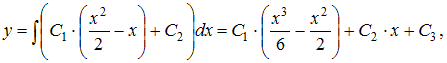
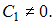
То есть общее решение имеет вид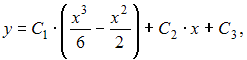
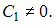
ответ тест i-exam
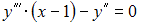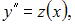
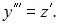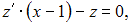
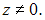
необходимо сделать замену Тогда порядок этого уравнения понизится на две единицы и оно примет вид Это уравнение первого порядка с разделяющимися переменными. Разделив переменные, получим:
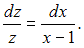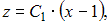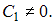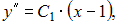
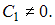
Тогда где Сделав обратную замену, получим дифференциальное уравнение Проинтегрируем последовательно обе части уравнения два раза:
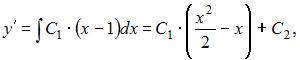
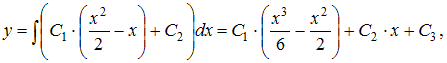
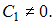
То есть общее решение имеет вид
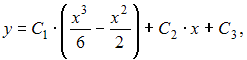
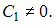
ответ тест i-exam