Предмет:
Тема:
Непрерывность функции, точки разрыва
Вопрос:
Для функции 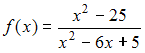 точка
точка 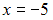 является точкой …
является точкой …
Ответы:
+ непрерывности
− разрыва второго рода
− разрыва первого рода
− устранимого разрыва
Решение:
Вычислим односторонние пределы функции 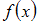 в точке
в точке 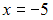 :
:
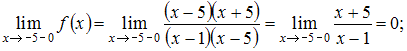
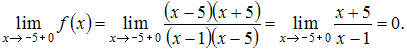
Так как и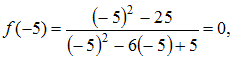 то есть
то есть 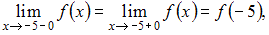 то точка
то точка 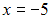 является точкой непрерывности данной функции.
является точкой непрерывности данной функции.
ответ тест i-exam
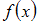 в точке
в точке 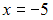 :
: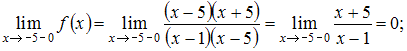
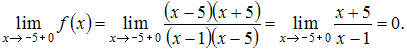
Так как и
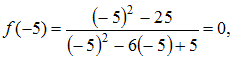 то есть
то есть 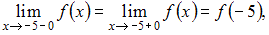 то точка
то точка 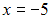 является точкой непрерывности данной функции.
является точкой непрерывности данной функции.ответ тест i-exam