Предмет:
Тема:
Динамика вращательного движения
Вопрос:
Диск может вращаться вокруг оси, перпендикулярной плоскости диска и проходящей через его центр. К нему прикладывают одну из сил (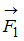
, 
, 
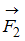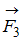или 
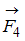), лежащих в плоскости диска и равных по модулю.
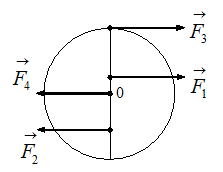
Верным для угловых ускорений диска является соотношение …
Ответы:
+ 
, 
, − 
− 
− 
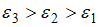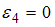
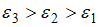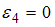
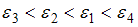
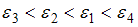
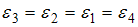
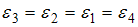
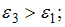
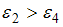
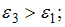
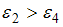
Решение:
Согласно основному уравнению динамики вращательного движения твердого тела относительно неподвижной оси угловое ускорение равно: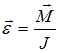 
. Отсюда следует, что угловое ускорение прямо пропорционально моменту приложенной к диску силы, который, в свою очередь, прямо пропорционален величине плеча силы (при условии равенства модулей сил). Таким образом, 
, 
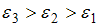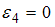, так как плечо силы 
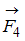равно нулю, и поэтому момент силы 
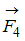равен нулю.
ответ тест i-exam
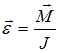. Отсюда следует, что угловое ускорение прямо пропорционально моменту приложенной к диску силы, который, в свою очередь, прямо пропорционален величине плеча силы (при условии равенства модулей сил). Таким образом, 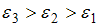, , 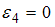так как плечо силы 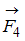равно нулю, и поэтому момент силы 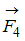равен нулю.ответ тест i-exam
Похожие вопросы:
, направленной перпендикулярно плоскости диска к «нам», и совершает гармонические крутильные колебания относительно вертикальной оси, проходящей через центр диска 
: 
, где 
– частота крутильных колебаний. Длина стержня 
, где 
и 
– расстояния от концов стержня до центра диска 
. Для определения максимальной разности потенциалов между концами стержня 
и 
необходимо учесть следующие справедливые утверждения:
и угловым ускорением 
, установлен на теле B, движущемся по горизонтальной направляющей согласно уравнению 
. Оси 
неизменно связаны с телом B, оси 
— неподвижные оси, точка M — некоторая точка диска. Движение диска (а вместе с ним и его тоски M) разложено на два движения и на основании теоремы о сложении ускорений для точки M в некоторый момент времени построен многоугольник ускорений.
и угловым ускорением 
, установлен на теле B, движущемся по горизонтальной направляющей согласно уравнению 
. Оси 
неизменно связаны с телом B, оси 
— неподвижные оси, точка M — некоторая точка диска. Движение диска (а вместе с ним и его тоски M) разложено на два движения и на основании теоремы о сложении ускорений для точки M в некоторый момент времени построен многоугольник ускорений.
и угловым ускорением 
, установлен на теле B, движущемся по горизонтальной направляющей согласно уравнению 
. Оси 
неизменно связаны с телом B, оси 
— неподвижные оси, точка M — некоторая точка диска. Движение диска (а вместе с ним и его тоски M) разложено на два движения и на основании теоремы о сложении ускорений для точки M в некоторый момент времени построен многоугольник ускорений.
и угловым ускорением 
, установлен на теле B, движущемся по горизонтальной направляющей согласно уравнению 
. Оси 
неизменно связаны с телом B, оси 
— неподвижные оси, точка M — некоторая точка диска. Движение диска (а вместе с ним и его тоски M) разложено на два движения и на основании теоремы о сложении ускорений для точки M в некоторый момент времени построен многоугольник ускорений.
и угловым ускорением 
, установлен на теле B, движущемся по горизонтальной направляющей согласно уравнению 
. Оси 
неизменно связаны с телом B, оси 
— неподвижные оси, точка M — некоторая точка диска. Движение диска (а вместе с ним и его тоски M) разложено на два движения и на основании теоремы о сложении ускорений для точки M в некоторый момент времени построен многоугольник ускорений.