Предмет:
Тема:
Ряд Фурье. Теорема Дирихле
Вопрос:
Разложение в ряд Фурье на промежутке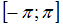 
существует для функции…
Ответы:
+ 
− 
− 
− 
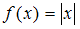
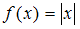
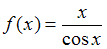
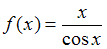
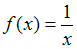
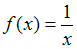
Решение:
Сформулируем условия Дирихле:
Если функция
периода 
кусочно-монотонна в промежутке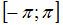 
и имеет в нем не более чем конечное число точек разрыва первого рода, то ее ряд Фурье сходится к сумме 
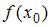в каждой точке непрерывности и к сумме 
в каждой точке разрыва.
Тогда разложение в ряд Фурье на промежутке
существует для функции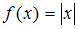 
, так как она удовлетворяет всем условиям Дирихле: функция 
непрерывна на 
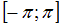и кусочно-монотонна на 
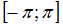, т.е. отрезок 
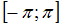можно разделить на два отрезка: 
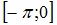- промежуток убывания и 
- промежуток возрастания.
Функции
, 
, 
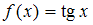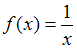имеют на промежутке 
разрывы второго рода, а значит, не разлагаются в ряд Фурье, так как по условиям Дирихле допускается конечное число точек разрыва первого рода.
ответ тест i-exam
Если функция
периода кусочно-монотонна в промежутке 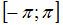и имеет в нем не более чем конечное число точек разрыва первого рода, то ее ряд Фурье сходится к сумме 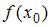в каждой точке непрерывности и к сумме в каждой точке разрыва. Тогда разложение в ряд Фурье на промежутке
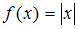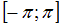существует для функции , так как она удовлетворяет всем условиям Дирихле: функция непрерывна на и кусочно-монотонна на 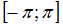, т.е. отрезок 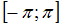можно разделить на два отрезка: 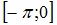- промежуток убывания и - промежуток возрастания.Функции
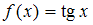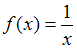, , имеют на промежутке разрывы второго рода, а значит, не разлагаются в ряд Фурье, так как по условиям Дирихле допускается конечное число точек разрыва первого рода.ответ тест i-exam