Предмет:
Тема:
Прямая линия в пространстве
Вопрос:
Даны прямая линия  , заданная уравнением
, заданная уравнением  , и плоскость
, и плоскость 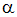 , заданная уравнением
, заданная уравнением 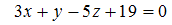 . Тогда прямая
. Тогда прямая 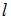 …
…
Ответы:
+ параллельна плоскости 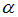
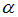
− принадлежит плоскости 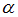
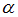
− перпендикулярна плоскости 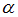
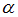
− пересекает плоскость 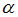 под острым углом
под острым углом
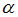 под острым углом
под острым угломРешение:
Направляющий вектор прямой имеет вид 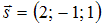 , а нормальный вектор плоскости
, а нормальный вектор плоскости 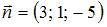 . Скалярное произведение этих векторов равно нулю:
. Скалярное произведение этих векторов равно нулю: 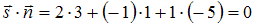 . Следовательно, прямая либо параллельна плоскости, либо принадлежит ей. Проверим условие принадлежности прямой плоскости. Для этого подставим координаты точки прямой
. Следовательно, прямая либо параллельна плоскости, либо принадлежит ей. Проверим условие принадлежности прямой плоскости. Для этого подставим координаты точки прямой 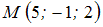 в уравнение плоскости:
в уравнение плоскости: 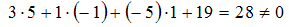 . То есть координаты точки прямой не удовлетворяют уравнению плоскости (точка не принадлежит плоскости). Таким образом, прямая
. То есть координаты точки прямой не удовлетворяют уравнению плоскости (точка не принадлежит плоскости). Таким образом, прямая 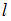 параллельна плоскости
параллельна плоскости 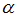 .
.
ответ тест i-exam
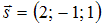 , а нормальный вектор плоскости
, а нормальный вектор плоскости 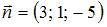 . Скалярное произведение этих векторов равно нулю:
. Скалярное произведение этих векторов равно нулю: 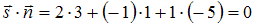 . Следовательно, прямая либо параллельна плоскости, либо принадлежит ей. Проверим условие принадлежности прямой плоскости. Для этого подставим координаты точки прямой
. Следовательно, прямая либо параллельна плоскости, либо принадлежит ей. Проверим условие принадлежности прямой плоскости. Для этого подставим координаты точки прямой 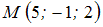 в уравнение плоскости:
в уравнение плоскости: 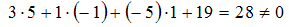 . То есть координаты точки прямой не удовлетворяют уравнению плоскости (точка не принадлежит плоскости). Таким образом, прямая
. То есть координаты точки прямой не удовлетворяют уравнению плоскости (точка не принадлежит плоскости). Таким образом, прямая 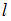 параллельна плоскости
параллельна плоскости 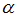 .
.ответ тест i-exam