Предмет:
Тема:
Напряжения в поперечном сечении стержня при плоском изгибе
Вопрос:
Однопролетная консольная балка прямоугольного сечения с размерами b и 2b нагружена силой F. Линейные размеры b и l = 20b заданы. В сечении I–I значение максимального касательного напряжения равно
Ответы:
+ 
− 
− 
− 
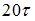
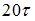
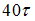
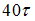
Решение:
Используя уравнения статики, определим реакции опор А и В: 
Касательное напряжение в любой точке поперечного сечения балки определяется по формуле Д. И. Журавского
Для прямоугольного сечения максимальное касательное напряжение возникает в точках на нейтральной линии и равно
где Q – значение поперечной силы в данном сечении; А – площадь поперечного сечения. В сечении I–I имеем 
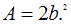
Тогда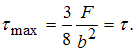
Максимальное нормальное напряжение возникает в сечении балки над опорой В, где действует максимальный изгибающий момент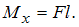
Значение максимального нормального напряжения вычислим по формуле 
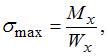где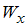 
– момент сопротивления.
Для прямоугольного сечения
После вычислений, учитывая, что
и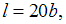 
получим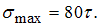 
ответ тест i-exam
Касательное напряжение в любой точке поперечного сечения балки определяется по формуле Д. И. Журавского
Для прямоугольного сечения максимальное касательное напряжение возникает в точках на нейтральной линии и равно
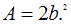
где Q – значение поперечной силы в данном сечении; А – площадь поперечного сечения. В сечении I–I имеем Тогда
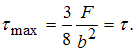
Максимальное нормальное напряжение возникает в сечении балки над опорой В, где действует максимальный изгибающий момент
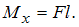Значение максимального нормального напряжения вычислим по формул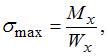е где 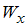– момент сопротивления.Для прямоугольного сечения
После вычислений, учитывая, что
и 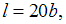получим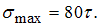 ответ тест i-exam
Похожие вопросы:
где d – диаметр образца цилиндрической формы (или 
где a и b – размеры сторон образцов прямоугольной формы). Для определения напряжения измеряются прикладываемое усилие F и диаметр образца d или размеры сторон a и b.
где d – диаметр образца цилиндрической формы (или 
где a и b – размеры сторон образцов прямоугольной формы). Для определения напряжения измеряются прикладываемое усилие F и диаметр образца d или размеры сторон a и b.
- наибольшая глубина потока в рассматриваемом живом сечении, м; 
- расстояние по уклону дна, м; 
- уклон дна; 
- расход потока, м3/с; 
- площадь живого сечения потока, м2; 
- коэффициент Шези, м1/2/с; 
- гидравлический радиус, м; 
– характерный поперечный размер, м; 
- ускорение свободного падения, м/с2; 
- коэффициент Кориолиса; 
- ширина живого сечения русла по верху, м
и 
, конденсаторов с емкостью 
и 
, резистора с сопротивлением 
. Амплитудные значения напряжения на катушках равны 
и 
, на конденсаторах - 
и 
, на резисторе - 
.
напряжения, приложенного к этой цепи, и сдвиг фаз между током и внешним напряжением определяются формулами: …
-площадь живого сечения, м2; 
- скорость фильтрации, м/с; 
- коэффициент фильтрации, м/с, 
– возвышение точки кривой депрессии, принадлежащей данному плоскому сечению, над произвольной горизонтальной плоскостью сравнения, величина представляет собой напор для рассматриваемого плоского вертикального сечения.