,
.Ответы:
+ ряд А) сходится условно, ряд В) сходится абсолютно
− ряд А) сходится условно, ряд В) сходится условно
− ряд А) расходится, ряд В) сходится абсолютно
− ряд А) расходится, ряд В) сходится условно
Решение:
Для исследования сходимости знакочередующегося ряда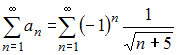 
применим признак сходимости Лейбница. Тогда:
1) вычислим предел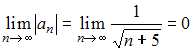
.
2) для любого натурального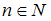
справедливо 
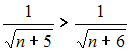, то есть последовательность 
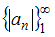монотонно убывает.
Следовательно, ряд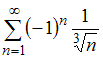
сходится.
Теперь проверим ряд на абсолютную сходимость. Для этого составим знакоположительный числовой ряд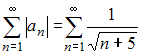
и исследуем его сходимость по теореме сравнения с расходящимся обобщенным гармоническим рядом 
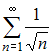. Тогда 
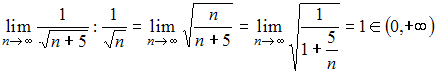. То есть ряд 
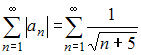расходится, следовательно, ряд 
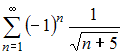сходится условно.
Теперь исследуем на сходимость ряд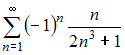
. Этот ряд сходится абсолютно, так как при применении теоремы сравнения со сходящимся обобщенным гармоническим рядом 
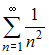, получаем:
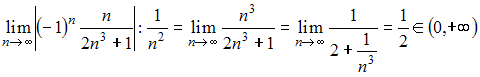. А это означает, что ряд 
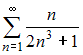сходится.
ответ тест i-exam
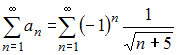применим признак сходимости Лейбница. Тогда:1) вычислим предел
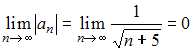.2) для любого натурального
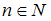справедливо 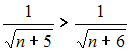, то есть последовательность 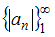монотонно убывает.Следовательно, ряд
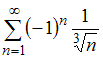сходится.Теперь проверим ряд на абсолютную сходимость. Для этого составим знакоположительный числовой ряд
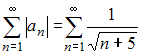и исследуем его сходимость по теореме сравнения с расходящимся обобщенным гармоническим рядом 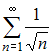. Тогда 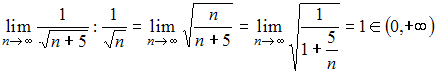. То есть ряд 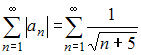расходится, следовательно, ряд 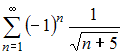сходится условно.Теперь исследуем на сходимость ряд
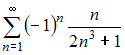. Этот ряд сходится абсолютно, так как при применении теоремы сравнения со сходящимся обобщенным гармоническим рядом 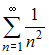, получаем: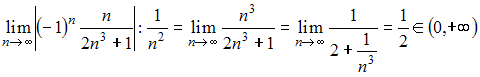. А это означает, что ряд 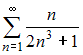сходится.ответ тест i-exam