Предмет:
Тема:
Поперечная сила, изгибающий момент и их эпюры
Вопрос:
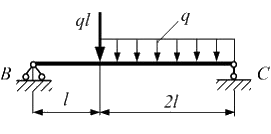
Однопролетная балка ВС длиной 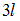 нагружена силой
нагружена силой 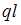 и равномерно распределенной нагрузкой интенсивности q. Максимальные значения изгибающего момента и поперечной силы по абсолютной величине соответственно равны …
и равномерно распределенной нагрузкой интенсивности q. Максимальные значения изгибающего момента и поперечной силы по абсолютной величине соответственно равны …
Ответы:
+ 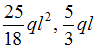
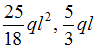
− 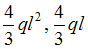
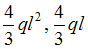
− 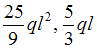
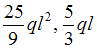
− 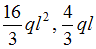
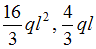
Решение:
Заменяем действие отброшенных на балку связей реакциями: 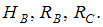
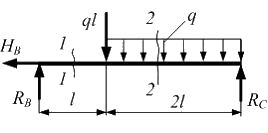
Используя уравнения статики, найдем: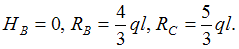
Балка имеет два участка. Для определения внутренних силовых факторов на каждом участке воспользуемся методом сечений. Рассекаем балку на левом участке произвольным сечением 1–1 и отбросим правую часть.
Рассмотрим равновесие левой оставшейся части. Действие отброшенной правой части заменяем на левую поперечной силой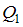 и изгибающим моментом
и изгибающим моментом 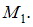 (Напоминаем, что при плоском поперечном изгибе в поперечном сечении балки возникают два внутренних силовых фактора: поперечная сила Q и изгибающий момент М).
(Напоминаем, что при плоском поперечном изгибе в поперечном сечении балки возникают два внутренних силовых фактора: поперечная сила Q и изгибающий момент М).
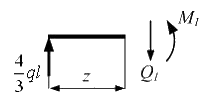
Переменная z отсчитывается от крайнего левого сечения и изменяется в пределах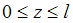 . Из уравнений равновесия получим
. Из уравнений равновесия получим 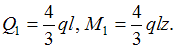
Следовательно, поперечная сила по длине первого участка постоянна, а изгибающий момент меняется по линейному закону. Вычислим значения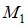 в начале и в конце участка
в начале и в конце участка 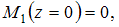
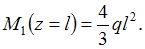
Затем рассекаем балку произвольным сечением 2–2 в пределах второго участка и рассмотрим равновесие правой части.
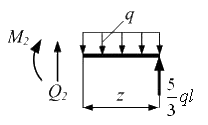
Переменная z отсчитывается от крайнего правого сечения и меняется в пределах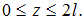
Из условий равновесия правой части найдем
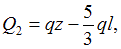
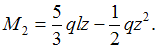
Поперечная сила по длине второго участка меняется по линейному закону, а изгибающий момент по закону квадратной параболы. Найдем значения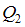 и
и 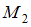 в начале и конце участка:
в начале и конце участка:
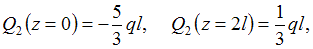
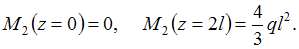
Из полученных значений для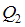 следует, что в некотором сечении второго участка поперечная сила
следует, что в некотором сечении второго участка поперечная сила 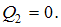 Положение данного сечения ( координату z) определим из уравнения
Положение данного сечения ( координату z) определим из уравнения 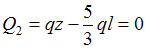 , отсюда
, отсюда 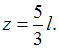
Выражение для изгибающего момента содержит переменную во второй степени. Поэтому исследуем функцию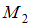 на аналитический экстремум
на аналитический экстремум
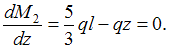
Следовательно, в сечении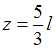 (в данном сечении поперечная сила равна нулю) изгибающий момент принимает экстремальное значение
(в данном сечении поперечная сила равна нулю) изгибающий момент принимает экстремальное значение 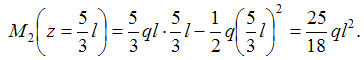
Сравнивая полученные значения поперечных сил и изгибающих моментов, делаем вывод, что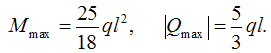
ответ тест i-exam
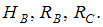

Используя уравнения статики, найдем:
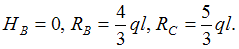
Балка имеет два участка. Для определения внутренних силовых факторов на каждом участке воспользуемся методом сечений. Рассекаем балку на левом участке произвольным сечением 1–1 и отбросим правую часть.
Рассмотрим равновесие левой оставшейся части. Действие отброшенной правой части заменяем на левую поперечной силой
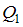 и изгибающим моментом
и изгибающим моментом 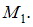 (Напоминаем, что при плоском поперечном изгибе в поперечном сечении балки возникают два внутренних силовых фактора: поперечная сила Q и изгибающий момент М).
(Напоминаем, что при плоском поперечном изгибе в поперечном сечении балки возникают два внутренних силовых фактора: поперечная сила Q и изгибающий момент М). 
Переменная z отсчитывается от крайнего левого сечения и изменяется в пределах
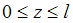 . Из уравнений равновесия получим
. Из уравнений равновесия получим 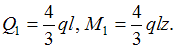
Следовательно, поперечная сила по длине первого участка постоянна, а изгибающий момент меняется по линейному закону. Вычислим значения
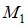 в начале и в конце участка
в начале и в конце участка 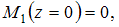
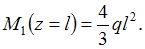
Затем рассекаем балку произвольным сечением 2–2 в пределах второго участка и рассмотрим равновесие правой части.
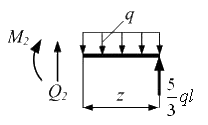
Переменная z отсчитывается от крайнего правого сечения и меняется в пределах
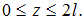
Из условий равновесия правой части найдем
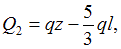
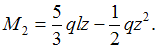
Поперечная сила по длине второго участка меняется по линейному закону, а изгибающий момент по закону квадратной параболы. Найдем значения
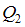 и
и 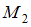 в начале и конце участка:
в начале и конце участка: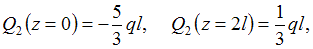
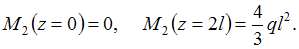
Из полученных значений для
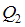 следует, что в некотором сечении второго участка поперечная сила
следует, что в некотором сечении второго участка поперечная сила 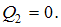 Положение данного сечения ( координату z) определим из уравнения
Положение данного сечения ( координату z) определим из уравнения 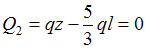 , отсюда
, отсюда 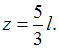
Выражение для изгибающего момента содержит переменную во второй степени. Поэтому исследуем функцию
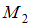 на аналитический экстремум
на аналитический экстремум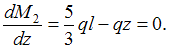
Следовательно, в сечении
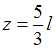 (в данном сечении поперечная сила равна нулю) изгибающий момент принимает экстремальное значение
(в данном сечении поперечная сила равна нулю) изгибающий момент принимает экстремальное значение 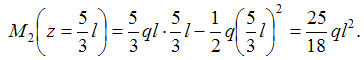
Сравнивая полученные значения поперечных сил и изгибающих моментов, делаем вывод, что
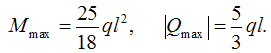
ответ тест i-exam