Предмет:
Тема:
Системы линейных уравнений
Вопрос:
Система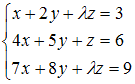 
совместна и неопределенна, если 
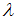равно …
Ответы:
+ 1
− 2
− – 1
− – 2
Решение:
Система линейных уравнений совместна, если ранг основной матрицы системы равен рангу расширенной матрицы.
Расширенная матрица системы имеет вид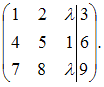
Вычислим минор третьего порядка этой матрицы не содержащий элемент 
:
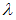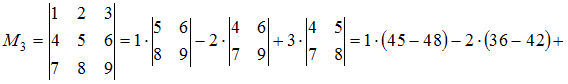
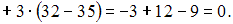Вычислим минор второго порядка этой матрицы не содержащий элемент 
: 
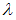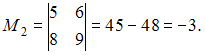Ранг расширенной матрицы равен двум. Тогда ранг матрицы системы должен быть равен двум (определитель матрицы системы равен нулю, так как минор второго порядка не равный нулю существует). Из этого условия находим 
:
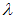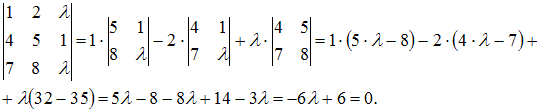
Значит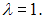
ответ тест i-exam
Расширенная матрица системы имеет вид
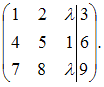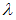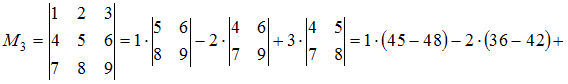
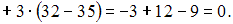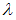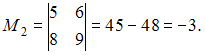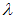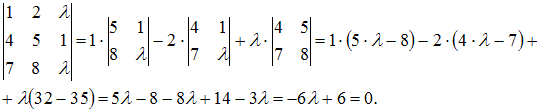
Вычислим минор третьего порядка этой матрицы не содержащий элемент : Вычислим минор второго порядка этой матрицы не содержащий элемент : Ранг расширенной матрицы равен двум. Тогда ранг матрицы системы должен быть равен двум (определитель матрицы системы равен нулю, так как минор второго порядка не равный нулю существует). Из этого условия находим :Значит
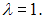
ответ тест i-exam