Предмет:
Тема:
Элементы гармонического анализа
Вопрос:
Функцией, ортогональной к функции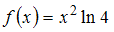 
на 
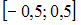, является …
Ответы:
+ 
− 
− 
− 
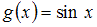
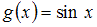
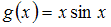
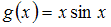
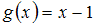
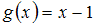
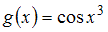
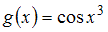
Решение:
Функци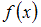и 
и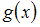 
называются ортогональными на [a, b], если 
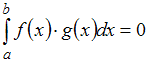. Функция 
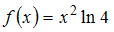на 
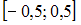является четной, поэтому функция 
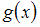в данной задаче должна быть нечетной, так как тогда произведение 
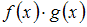будет нечетной функцией, а интеграл от нечетной функции по симметричному интервалу равен нулю.
Проверим функции на нечетность:
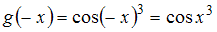– четная функция;
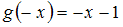– функция общего вида;
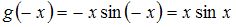– четная функция;
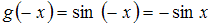– нечетная функция.
Тогда функцией, ортогональной к функции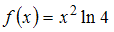
на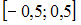 
, может служить 
.
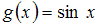ответ тест i-exam
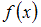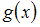и называются ортогональными на [a, b], если 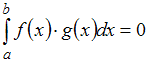. Функция 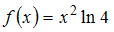на 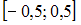является четной, поэтому функция 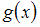в данной задаче должна быть нечетной, так как тогда произведение 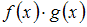будет нечетной функцией, а интеграл от нечетной функции по симметричному интервалу равен нулю.Проверим функции на нечетность:
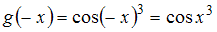– четная функция; 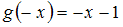– функция общего вида; 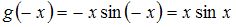– четная функция; 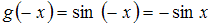– нечетная функция.Тогда функцией, ортогональной к функции
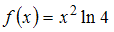на 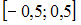, может служить 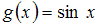.ответ тест i-exam