Предмет:
Тема:
Задача Коши для дифференциального уравнения первого порядка
Вопрос:
Решение задачи Коши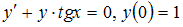 
, имеет вид …
Ответы:
+ 
− 
− 
− 
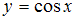
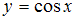
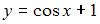
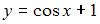
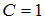
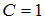
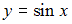
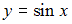
Решение:
Запишем уравнение в виде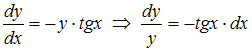 
. Проинтегрировав обе части, получим: 
.
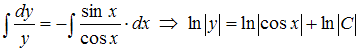Тогда общее решение исходного уравнения имеет вид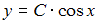
. Для вычисления значения 
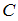подставим в найденное общее решение начальное условие 
.
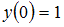Тогда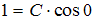
и 
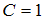. Следовательно, частное решение имеет вид 
.
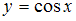ответ тест i-exam
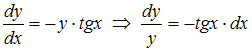. Проинтегрировав обе части, получим: 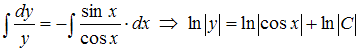.Тогда общее решение исходного уравнения имеет вид
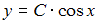. Для вычисления значения 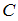подставим в найденное общее решение начальное условие 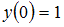.Тогда
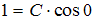и 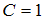. Следовательно, частное решение имеет вид 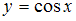.ответ тест i-exam